计组考前复习

发表于 更新于 分类于 本文字数： 4.1k 阅读时长 ≈ 15 分钟

其实应该叫 ICS, 计算机系统基础复习, 但这门课下次就改名了, 教材也选用的是计组(谭志虎, 是好书)的, 我不好说.

明明不做配套的实验, 让学生干瞪数字电路多少有些抽象. 而且大部分时间讲的还是前半部分...求求改考 CSAPP 吧, 我什么都会做的.

upd: 没复习的三章考了 40 多分, 自己觉得重要的部分忘了差不多, 等死.

计算机系统概述

基础知识

摩尔定律: 当价格不变时, 集成电路上可容纳的晶体管数目, 约 18 个月会增加一倍, 性能也将提升一倍.

计算机系统的层次结构

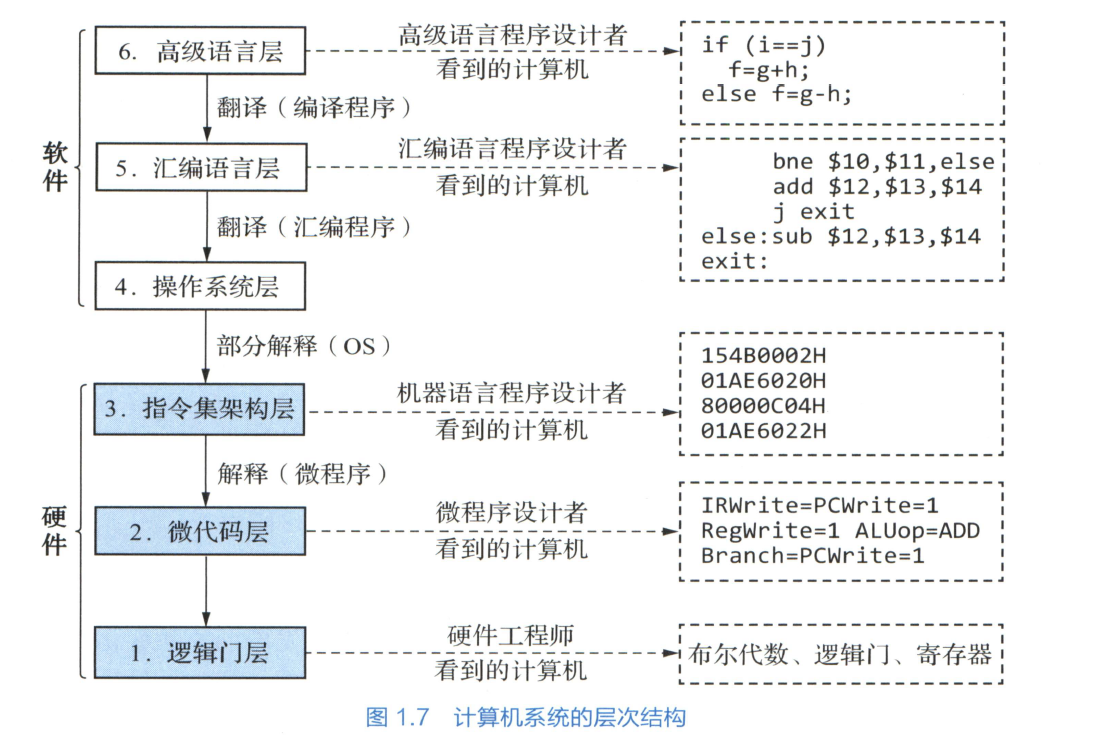
计算机系统的层次结构

汇编器: 将汇编语言程序翻译为机器语言程序

编译器: 将高级语言程序翻译为汇编语言或机器语言程序

性能指标: 字长, 主存容量单位, 时钟周期, CPI, IPC, CPU时间, MIPS, TFLOPS

  • 字长: CPU 一次处理的数据位数
  • 主存容量: 单位 KB, MB, GB, TB, PB
  • 时钟周期: CPU 完成一个最基本动作的时间. 例如主频 1Ghz 就是 1ns.
  • CPI, Clock Cycles Per Instruction: 执行每条指令所需的平均时钟周期数.
  • CPU 时间: 程序在处理器上实际运行的时间
  • IPC: 每个时钟周期 CPU 能执行的指令条数. CPI 的倒数. IPC 可以大于 1.
  • MIPS: 每秒百万条指令
  • MFLOPS: 每秒执行百万次浮点运算
  • TFLOPS: 单位变成 T, 是标志显卡运算能力的一个常用指标

总指令条数记为 IC, 程序执行所需时钟周期数 \(m\), 时钟周期 \(T\), 频率为 \(f\)

\[\mathrm{CPI}=\sum_{i=1}^{n}(\mathrm{~CPI}_{i}\times P_{i})=\sum_{i=1}^{n}(\mathrm{~CPI}_{i}\times\frac{\mathrm{IC}_{i}}{\mathrm{IC}})\]

\[T_{\mathrm{cpu}}=m\times T=\frac mf\]

\[\mathrm{MIPS}=\frac{f}{\mathrm{CPI}}=\mathrm{IPC}\times f\]

\[\mathrm{MFLOPS}=\frac{\mathrm{IC}_{\mathrm{flops}}}{T_{\mathrm{cpu}}\times10^{6}}\]

例题

例题 1.1 计算指标

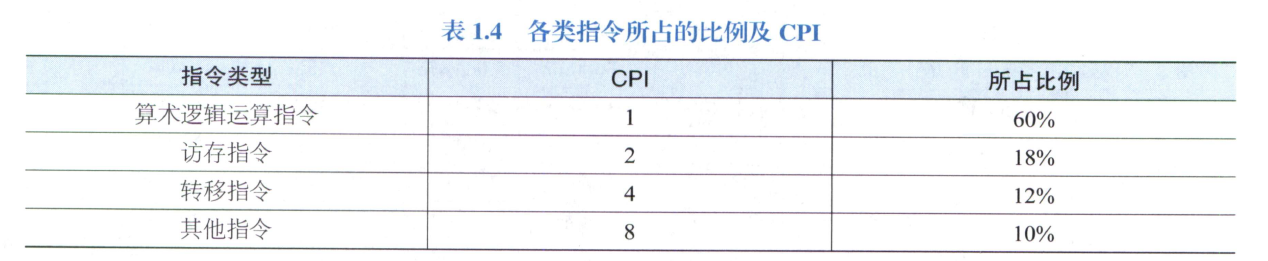
各类指令所占比例
  1. 求程序的 CPI
  2. 若 CPU 的主频为 400 MHz, 求机子的 MIPS.

解

\[\mathrm{CPI}=\sum_{i=1}^{n}(\mathrm{CPI}_{i}\times P_{i})=1\times0.6+2\times0.18+4\times0.12+8\times0.1=2.24\]

\[\mathrm{MIPS}=\frac{f}{\mathrm{CPI}}=\frac{400}{2.24}=178.6\]

例题 1.2 A 和 B 基于相同指令集设计的两种类型的计算机, A 的时钟周期为 2ns, 某程序在 A 上运行时的 CPI 为 3, B 的时钟周期为 4ns, 同一程序在 B 上的 CPI 为 2, 对于这个程序而言, 哪个电脑跑的更快.

\[T_{\mathrm{cpuA}}=\mathrm{CPI}_{\mathrm{A}}\times\mathrm{IC}\times T_{\mathrm{A}}\quad T_{\mathrm{cpuB}}=\mathrm{CPI}_{\mathrm{B}}\times\mathrm{IC}\times T_{\mathrm{B}}\]

\[\frac{T_{\mathrm{cpuA}}}{T_{\mathrm{cpuB}}}=\frac{\mathrm{CPI}_{\mathrm{A}}\times\mathrm{IC}\times T_{\mathrm{A}}}{\mathrm{CPI}_{\mathrm{B}}\times\mathrm{IC}\times T_{\mathrm{B}}}=\frac{3\times\mathrm{IC}\times2}{2\times\mathrm{IC}\times4}=0.75\]

例题 1.3 三种指令在某一计算机上的 CPI

指令 A B C
CPI 1 2 3

两种不同的编译器将同一高级语言的语句编译为两种不同类型的代码序列, 如下表所示

代码序列 A B C
1 2 1 2
2 4 1 1
  1. 两种代码序列的 CPI 分别是多少.
  2. 哪种代码执行速度更快.

解

\[\begin{aligned}\mathrm{CPI}_1=&1\times\frac{2}{5}+2\times\frac{1}{5}+3\times\frac{2}{5}=2\\\\\mathrm{CPI}_2=&1\times\frac{4}{6}+2\times\frac{1}{6}+3\times\frac{1}{6}=1.5\end{aligned}\]

\[T_{\mathrm{cpu1}}=2\times5\times T=10T\quad T_{\mathrm{cpu2}}=1.5\times6\times T=9T\]

数据信息的表示

原码, 反码, 补码(定点小数, 定点整数)

反码法, 扫描法

其实就是利用一个式子 \(-i=\sim i+1\) 去得到补码表示, 还要给他们起名字😓

移码Offset binary, 补码到移码

IEEE754浮点数表示法

IEEE754浮点数表示法
  • S:E:M=1:8:23
  • 阶码是移码表示, 偏移量 127
  • M 定点小数, 带一个 implied leading 1, 实际有效位是 24
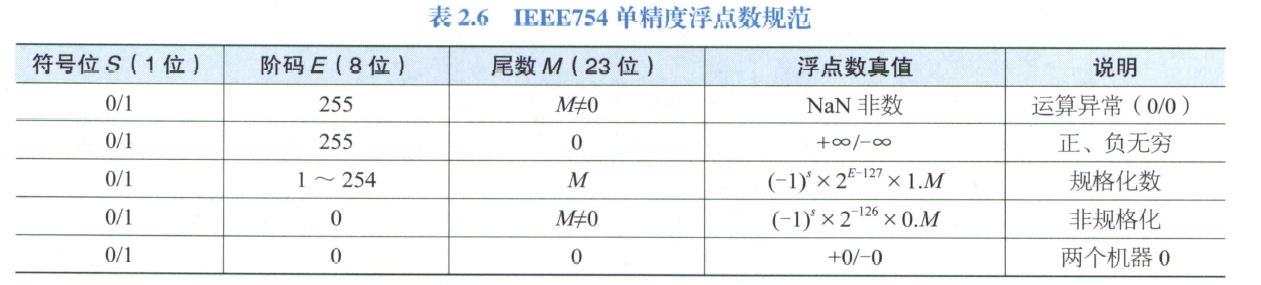
单浮点数规范

规格化数

\[N=(-1)^s\times2^{E-127}\times1.M\]

单浮点数表示范围

IEEE754浮点数和真值之间的转换关系

8421, 2421, 余三码, BID 码, DPD 码

新考研大纲里不考了, 了解即可. 学校考试真考我就把他给冲了.

基于 C 语言的数据表示转换

  • C 语言里的数据表示, overflow, convertion

码距: 海明距离

例如 1010 到 0101 的码距就是 4

奇偶校验码, 海明码的分组设计, 拓展海明码, CRC 编码

例题

补码和其它码表示之间的相互转换

通常转换的是负数和小数

设 \(x=-1000\), 则 \(x_补=10111+0001=11000\) (反码法)

扫描法: 对于 \(x<0\) 的, 右起第一个 1 和右边的 0 不变, 其它位 flip

例如 \(x=-1000\), 则 \(x_补=11000\), \(-0.0001\) 补码 \(x_补=1.1111\)

Remark: 记这些花里胡哨的有屁用😓 用定义不好吗?

例题 2.7 写出 20.59375 的单精度浮点数的十六进制机器码.

\((20.59375)_{10}=(10100.10011)_2=(1.010010011)\times 2^{4}\)

于是 \(S=0\), \(E=e+127=4+127=131=10000011\), \(M=010010011\)

最终的机器码 \((0100 0001 1010 0100 1100 0000 0000 0000)_2=(41A4C000)_{16}\).

例题 2.9 \(f(n)=\sum_{0}^{n}2^i=11...1B\), 计算 \(f(n)\) 的 C 程序如下

1
2
3
4
5
6
7
8
9
10
int f1(unsigned int n)
{
    int sum = 1, power = 1;
    for (unsigned i = 0; i <= n - 1; i++)
    {
        power *= 2;
        sum += power;
    }
    return sum;
}

将上面的 int 都改成 float, 可得到 f2.

  1. \(n = 0\) 为什么会出现死循环. 改成 int 又会怎样?
  2. f1(23) 和 f2(23) 的返回值相同吗? 机器数分别是什么?
  3. f1(24) 和 f2(24) 的返回值分别为 33 554 431 和 33554532.0, 为什么不等.
  4. \(f1(31)=2^{32}-1\), 而 \(f1(31)\) 的返回值是 -1, 为什么. 或者你能给出 \(n\) 的一个范围吗.
  5. f2(127) 的机器数为 7F80 0000H, 对应的值是什么. 若要使得 f2(n) 的值不溢出, 最大的 n 是多少.

解 n=0 的情况, n-1 就是 UMax, i 永远小于等于这个值. 改成 int 就没事了.

f(23) = 1111 1111 1111 1111 1111B, 就是 24 个 1, int 塞得下, float 尾数也可以塞得下.

  • f1(23) = 00FF FFFF
  • f2(23) = 4B7F FFFF

n = 24 时, 对于 float 舍入后数值增大, 此时浮点数的最小刻度是 2, 所以 f2(24) 要比 f1(24) 大 1.

\(n\) 最大 30. (如果改成了 int 的话)

阶码255, 尾数0, 表示 inf. 不溢出 \(n\) 的最大值是 126.

例题 2.11 \(D_7\dots D_2D_1=1101010\), 给出能纠正一位错的海明码方案. 有 3 位错的前提下, 分析能否区分一位错和两位错.

解 分组

\[\begin{matrix}\mathrm{Gl(P_1,~D_1,~D_2,~D_4,~D_5,~D_7)}&\mathrm{G2(P_2,~D_1,~D_3,~D_4,~D_6,~D_7)}\\\mathrm{G3(P_3,~D_2,~D_3,~D_4)}&\mathrm{G4(P_4,~D_5,~D_6,~D_7)}\end{matrix}\]

\[\begin{aligned}\mathrm{P}_1&=\mathrm{D}_1\oplus\mathrm{D}_2\oplus\mathrm{D}_4\oplus\mathrm{D}_5\oplus\mathrm{D}_7=0\oplus1\oplus1\oplus0\oplus1=1\\\mathrm{P}_2&=\mathrm{D}_1\oplus\mathrm{D}_3\oplus\mathrm{D}_4\oplus\mathrm{D}_6\oplus\mathrm{D}_7=0\oplus0\oplus1\oplus1\oplus1=1\\\mathrm{P}_3&=\mathrm{D}_2\oplus\mathrm{D}_3\oplus\mathrm{D}_4=1\oplus0\oplus1=0\\\mathrm{P}_4&=\mathrm{D}_5\oplus\mathrm{D}_6\oplus\mathrm{D}_7=0\oplus1\oplus1=0\end{aligned}\]

\[\mathrm H_{11}\cdots\mathrm H_2\mathrm H_1=\mathrm D_7\mathrm D_6\mathrm D_5\mathrm P_4\mathrm D_4\mathrm D_3\mathrm D_2\mathrm P_3\mathrm D_1\mathrm P_2\mathrm P_1=11001010011\]

如果 \(D_6, D_7\) 同时出错, \(G_4\) 发生偶数位错, \(G_3\) 无错误, \(G_2\) 发生偶数位错误, \(G_1\) 发生一位错误, 最终的错误码 \(0001\), 和 \(G_1\) 中的校验位 \(P_1\) 出错是相同的, 所以不能区分一位错和两位错. 可以通过引入总偶校验位来解决.

例题 2.14 求有效信息 110 的 CRC 码, 生成多项式 \(G(x)=11101\).

\(M(x)\cdot 2^4 = x^6 + x^5 = 110 0000\), 按模 2 除法 11101, 得到商 \(101\) 和余数 \(1001\). 最后的 CRC 码 \(110 1001\).

运算方法与运算器

补码的加减法规则; 基于补码的溢出判定

单符号位的检测

\[V=A_{\mathrm{s}}B_{\mathrm{s}}\overline{S_{\mathrm{s}}}+\overline{A_{\mathrm{s}}}\overline{B_{\mathrm{s}}}S_{\mathrm{s}}\]

双符号位

  • \(S_{s1}S_{s2} = 00\): 无溢出
  • \(S_{s1}S_{s2} = 10\): 正溢出
  • \(S_{s1}S_{s2} = 10\): 负溢出
  • \(S_{s1}S_{s2} = 11\): 结果为负数, 无溢出

全加器的电路实现, 可控加减法电路

\[C_{i+1}=X_iY_i+(X_i\oplus Y_i)C_i\]

  • 每一位的运算结果 \(X_i \oplus Y_i \oplus C_i\)
  • \(C_i\) 是进位
  • \(C_{i + 1} = X_iY_i + (X_i \oplus Y_i)C_i\)

串行进位加法

先行进位加法

  • 把 \(G_i=X_iY_i\) 和 \(P=X_i\oplus Y_i\) 先行计算
  • 把 \(C_i\) 先计算出来
  • 这样后面每一位计算都是并行的
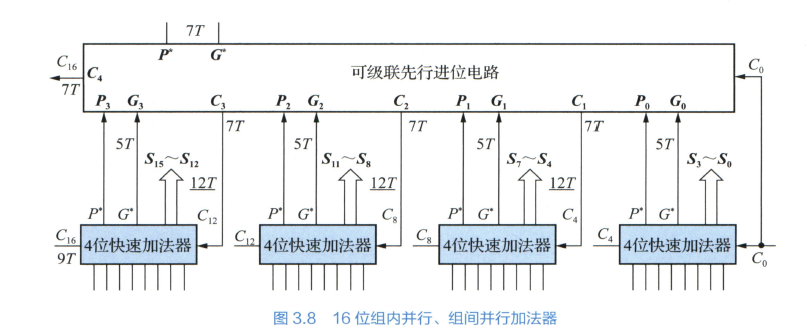
先行进位加法器的基本原理

先行计算电路级联

  • 组内并行, 组间并行加法器
  • 进一步并行
  • 传入 \(C_0\), 用一个额外的电路快速计算 \(C_4, C_8, C_{12}, C_{16}\)

原码一位乘法的基本原理

\[P_{i+1}=(P_i+y_{n-1}|x|)2^{-1}\]

补码一位乘法的基本原理(Booth 算法的推导)

\[P_{i+1}=(P_i+(y_{n-i+1}-y_{n-i})[x]_\text{补})2^{-1}\]

\[[x\times y]_\text{补}=P_{n+1}=P_n+(y_1-y_0)[x]_\text{补}\]

注意 Booth 算法去计算补码一位乘法, 第一步会人为给 \(y\) 添加一个 \(y_{n+1}=0\) 的一位.

原码恢复, 不恢复余数法计算两个数的商和余数

原码不恢复余数法, 加减交替法 \([x]_原/[y]_原\)

  • 先用被除数减去除数 \(|x|-|y|=|x|+(-|y|)=|x|+[|-y|]_补\)
    • 余数为正, 商加 1. 余数和商左移一位, 再减去除数.
    • 余数为负, 商上 0, 余数和商左移一位, 再加上除数.
  • 第 \(n+1\) 步余数为负的时候, 加上 \(|y|\) 得到第 \(n+1\) 正确的余数.

补码的加减交替法

  • 每一步考虑中间余数是否和 \([y]_补\) 同号
  • 注意末尾恒置 1 (不考虑精度的情况)

浮点数加减运算中的舍入规则

  • 对阶
  • 尾数运算
  • 结果规范化
  • 舍入
    • 末尾恒置 1 法: 丢失的有一位是 1, 就把运算的最低结果置为 1
    • 0 舍 1 入法: 丢失位数的最高位是 1, 就将尾数的末位加 1
  • 溢出判断

例题

(2020 统考题) 有实现 \(x\times y\) 的两个 C 语言函数如下:

1
2
unsigned umul(unsigned x, unsigned y) { return x * y; }
int imul(int x, int y) { return x * y; }

假设某计算机 M 中的 ALU 只能进行加减运算和逻辑运算, 回答下面问题:

  1. 若 M 的指令系统没有乘法指令, 但有加法减法和位移等指令, 则在 M 上也可以实现上述两个函数中的乘法运算, 为什么?
  2. 若 M 的指令系统有乘法指令, 基于 ALU, 位移器, 寄存器和相应逻辑实现乘法指令时, 控制逻辑的作用是什么?
  3. 针对下面三种情况 a) 没有乘法指令 b) 有 ALU 和位移器实现的乘法指令 c) 有阵列乘法器实现的乘法指令, umul 在哪种情况下的执行时间最长?
  4. \(n\) 位乘法指令可保存 \(2n\) 位乘积, 当仅取低 \(n\) 位作为乘积时, 其结果可能会发生溢出. \(n=32, x=2^{32}-1,y=2\) 时, imul 和 umul 得到的 \(x\times y\) 的 \(2n\) 位乘积分别是什么? 此时两者的返回结果是否溢出? 对于无符号整数乘法运算, 当仅取乘积的低 \(n\) 位作为乘法结果时, 如何用 \(2n\) 位乘积进行溢出判断?

解 编译器可以将乘法转换成一个循环代码段, 通过比较, 加法和移位实现乘法.

控制逻辑是用来控制循环次数, 控制加法和移位操作.

a 最长, c 最短. 对于 b, c 都只需要一个乘法指令完成, 但是 b 无法在一个时钟周期内完成.

两个的结果都应是 0000 0000 FFFF FFFE, 对于 int 而言上溢了, 对于 unsigned 可以容纳. 我们考虑如果高 n 位都是 0 那么就不溢出.

存储系统

理解存储系统的层次结构

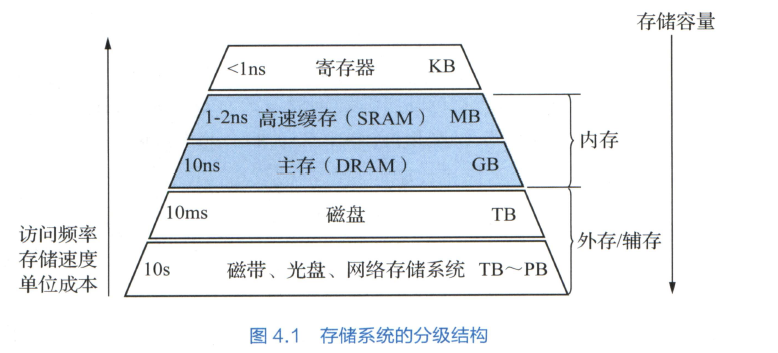
存储系统的层次结构

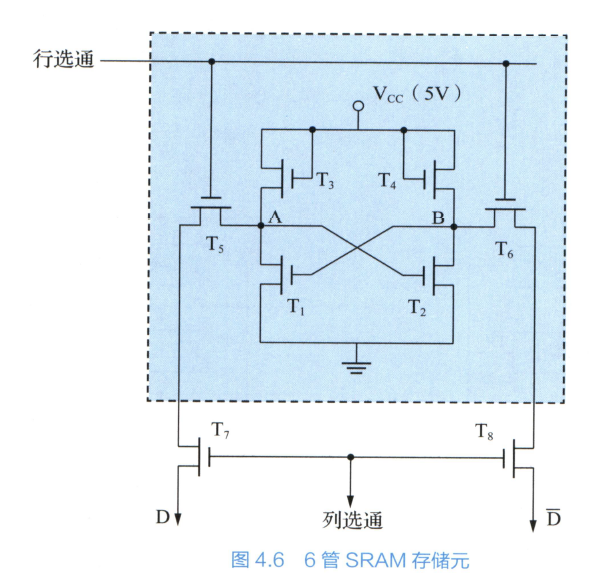
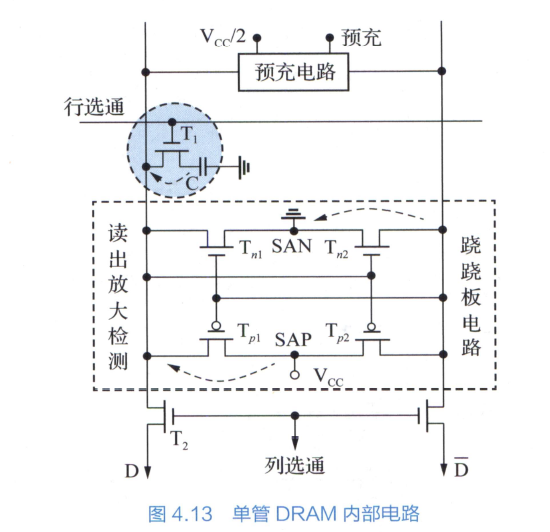
SRAM 和 DRAM 基本存储单元的结构和存储读取原理

SRAM
DRAM

存储单元的行列扩展方法 (位扩展、字扩展)

  • 位扩展, 字长扩展: 只加大字长, 存储器的字数和存储器芯片的字数一致.
  • 字扩展: 字的扩充, 位数不变.

也可以字位同时扩展

缓存的基本结构 (理解全相联, 直接相联, 组级联映射)

  • 全相联: 各个主存块都可以映射到 cache 的任意数据块
  • 直接相连: 各主存块只能映射到 cache 中的固定块
  • 组相联: 各主存块只能映射到 cache 中固定组的任意块

或者可以考虑各个组的大小分别为 n, 1, 1~n

写回和写穿策略

常见的缓存替换算法(FIFO, LFU, LRU, 随机替换)

有关存储的 对应 CSAPP 第六章

虚拟地址到物理地址的转换过程

  • 页表中的页表项数量和 VA 的 page number 字段长度相关, 例如 20bit 那就是 \(2^{20}\) 个, 不是比值

基于 TLB 的加速虚拟地址转换

就类似于给页表加一个 cache, 可以是组相联的

这里 VPO=tag+index

对应 CSAPP 第九章

例题

例题 4.3 某计算机字长为 32 位, 主存容量为 4 MB, 按字节编址, cache 采用直接相连映射, cache 容量为 4 KB, cache 块长度为 8 字.

  1. 画出直接相连映射下主存字节的划分情况, 并说明每个字段位数.
  2. 设 cache 的初始状态为空, 若 CPU 依次访问主存, 从 0 到 99 号单元并从中读出 100 个字(假设访问主存一次读出一个字)并重复此顺序 10 次, 计算 cache 访问的命中率.
  3. 如果 cache 的存取时间为 20 ns, 主存的存取时间为 200 ns, 根据 2) 中计算出的命中率求平均存取时间.
  4. 计算 cache/主存系统的访问效率.
主存字节地址

  1. 一个 cache 块(数据块副本的大小)包含 \(8\times 32 Bit = 32 B\), 因此 \(w=5\). cache 的存储体又被分为 \(4096B/32 B=128\) 行, 于是 \(r=7\)(需要 7 位去表示组索引). 访问 4 MB 主存空间需要 22 位地址线, 区地址(tag)长度 \(22-5-7=10\) 位.

  2. cache 有 128 行, 每行 8 个字, 初始为空, 那么主存从 0 开始到 99 号单元的 100 个字会载入 cache 前 13 行中(最后一行只包含 96~99, 共 4 个字)

第一次访问, 每个数据块的第一次读访问都不命中, 会将对应数据块载入(8个字全写入), 后续相邻的 7 次访问都会命中. 而后续的 9 次循环, 所有数据访问都会命中. 命中率的计算 \(h=(100\times 10 -13)/(100\times 10)=98.7\%\).

  1. \(T=0.987\times20\mathrm{ns+}(1-0.987)\times200\mathrm{ns}=22.34\mathrm{ns}\)

  2. \(e=20/22.34=89.5\%\)

例 4.6 设主存容量为 16 MB, 按字节寻址; 虚拟存储器容量为 4 GB, 采用页式虚拟存储器, 页面大小为 4 KB:

  1. 计算物理页号, 页内偏移, 虚拟页号字段各位多少位.
  2. 计算页表中页表项的数量.
  3. 若部分页表内容如下表所示, 求对应于虚拟地址(00015240)H 和 (03FFF180)H 的物理地址.
虚页表 有效位 买页号 虚页号 有效位 实页号
00010H 0 002H 03FFFH 0 1
00015H 1 035H ... ... ...

解 (1) 页面大小为 4 KB, 因此页偏移字段的位数为 12 位, 物理页号字段的位数位 24-12=12 位, 虚拟页号字段的位数为 32-12=20 位.

  1. 页表项数量与虚拟页号字段的位数相关, 虚拟页号字段为 20 位, 页表项数量为 \(2^{20}\) 项.

  2. 从虚拟地址(00015240)H 和 (03FFF180)H 中分离出的 20 位虚页表分别为 00015H 和 03FFFH. 查页表可知虚页表 00015H 对应的物理页表为 035H, 而与 03FFFH 对应的页不在主存中, 因为对应有效位为 0.

指令结构

MIPS 指令的结构, 常用指令的功能

中央处理器

单总线结构处理器

单周期结构处理器

多周期结构处理器

硬布线控制器

指令流水线

理解在流水线中的执行过程

理解流水线中的冲突与对应处理方式