从零开始的数据分析

发表于 更新于 分类于 本文字数： 6.7k 阅读时长 ≈ 24 分钟

从零开始的数据分析!

为啥开这个坑? 第一, 这学期上了这门课, 但感觉教授的内容好浅. 想要在这个领域多扩展些知识. 第二, 后端发展路线上确实有对数据分析的一点要求, 就当是提升自己的硬实力. 别的不说, 这门课是和量化交易相对而言最接近的课.

最后一点, 我是算法竞赛败犬. Regional Cu, Fe 屁用没有, 思来索去, 得出了一个观点: 卷不动 XCPC 那就赶紧跑路 (bushi1

其实可以认为这篇文章浓缩了整个学期课程最核心的内容 :)

配环境

WSL2 + Miniconda + Jupyter Lab

WSL2 参考微软文档. BTW 我是 Ubuntu 22.04 的发行版

Miniconda 安装: 文档

1
2
3
4
mkdir -p ~/miniconda3
wget https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-x86_64.sh -O ~/miniconda3/miniconda.sh
bash ~/miniconda3/miniconda.sh -b -u -p ~/miniconda3
rm -rf ~/miniconda3/miniconda.sh

执行 .sh 文件的时候会问你要不要改动安装路径之类. 一路 yes 默认配置就完了.

完事了以后编辑下 ~/.bashrc

1
2
3
4
5
# set conda path
export PATH=$PATH:/home/besthope/miniconda3/bin

# set default redirect explorer
export BROWSER="/mnt/c/'program files (x86)'/microsoft/edge/application/msedge.exe"

然后 source ~/.bashrc 让它激活.

第二步我们之后会用到: 让 jupyter 打开的浏览器重定向到 Edge. 当然你喜欢也可以改成 Windows 底下 Chrome, Firefox 的路径(记得是/mnt/开头).

看到提示符前面出现了一个 (base) 就说明 miniconda 环境配置好了. 但这个 base 看着急眼, 可以把这个设置关了:

1
conda config --set auto_activate_base false

可以试下

1
~/miniconda3/bin/conda init bash

bash 换成 zsh 也可以(如果你用的是 zsh 的话).

之后你就可以用 conda install 来装包了. 先把 jupyter lab 装了(你喜欢也能用 notebook):

1
conda install jupyterlab

或者激活了 conda 环境后用 pip 安装也可以.

此外, 你可能要装的有且不限于:

1
2
3
conda install Scikit-Learn
conda install matplotlib
conda install pandas

数据爬取

Request 库简介

我们会用到 Requests 这一个库: 它的底层是将 urllib3 进行了一定的封装, 使用起来更为简便同时强大. 同时, 也可以利用它来写后端接口的测试函数.

GET 方法去请求一个 URL

1
2
import request
response = requests.get(url)

我们得到一个 Response 对象, 从这个对象可以获取我们需要的全部信息.

1
2
response.text # 获取响应文本
response.encoding # 获取编码形式
1
2
3
# post 请求, 带数据
# 例如 token
r = requests.post('http://httpbin.org/post', data = {'key':'value'})
1
2
3
# 传递参数
>>> payload = {'key1': 'value1', 'key2': 'value2'}
>>> r = requests.get("http://httpbin.org/get", params=payload)

反爬处理

部分网站会有反爬虫的机制. 例如, 部分网站会屏蔽掉无 header 的请求

1
2
3
4
5
>>> r = requests.get("https://guba.eastmoney.com/news,zssh000001,1361469289.html")
>>> r.status_code
403
>>> r.text
'<html>\r\n<head><title>403 Forbidden</title></head>\r\n<body>\r\n<center><h1>403 Forbidden</h1></center>\r\n<hr><center>Microsoft-IIS/10.0</center>\r\n</body>\r\n</html>\r\n'

相应的, 在浏览器中找到 Agent

找到请求头 
1
2
header = {"Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/120.0.0.0 Safari/537.36 Edg/120.0.0.0"}
r = requests.get(url, headers=headers)

就可以爬取到对应网站的数据了.

如何绕开机制是数据爬取最关键的一步. 困难的需要一定逆向工程和浏览器调试能力, 我们以一个国内网站为例: 如何获取前 3 页网站的内容?

关注到一点, 当我们进入到第三页的时候, 实际上访问的 URL 没有改变. 我们审查表单元素, 然后找到了这个表单的刷新方式

1
2
3
4
5
<form id="mainForm" method="post" action="/perxxgkinfo/syssb/xkgg/xkgg!licenseInformation.action">
            <input type="hidden" name="page.pageNo" id="pageNo" value="3" />
            <input type="hidden" name="page.orderBy" id="orderBy" value="" />
            <input type="hidden" name="page.order" id="order" value="" />
            <input type="hidden" name="tempReportKey"  value="5b5ec86eeae44460af456144eed0ca62" />

也就是这个表单依然是通过 POST 方法获得, 但是它带有一些额外的参数:

  • page.pageNo: 网站的页数
  • tempReportKey: 翻页的密钥
    • 每一页会生成一个临时的 Key, 翻页的时候会验证 key
1
2
3
4
5
6
7
function jumpPage2(pageNo) {
  $("#pageNo").val(pageNo);
  if ($("#keys").val() == "请输入文件号、标题...") {
    $("#keys").val("");
  }
  $("#mainForm").submit();
}

剩下 orderBy 和 order 默认为空. 这个和 query 请求相关, 不管.

在浏览器里, 我们可以更直观地看到请求的表单数据

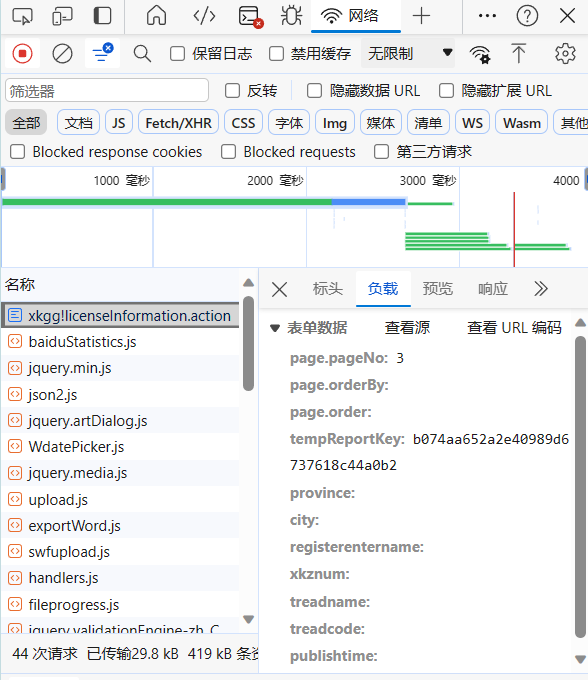
请求的表单数据

我们可以尝试通过添加这些表单数据进行请求

1
2
3
4
5
6
7
8
9
10
11
12
13
url = "http://permit.mee.gov.cn/perxxgkinfo/syssb/xkgg/xkgg!licenseInformation.action"
data = {"page.PageNo" : "1",
        "page.OrderBy" : "",
        "page.order" : "",
        "province" : "",
        "city" : "",
        "tempReportKey" : "",
        "registerentername" : "",
        "xkznum" : "",
        "treadname" : "",
        "treadcode" : "",
        "publishtime" : ""}
headers = {'User-Agent':'Mozilla/5.0 (X11; Linux x86_64; rv:102.0) Gecko/20100101 Firefox/102.0'}
1
2
3
4
5
6
7
8
9
10
11
12
13
html_pages = []
# 第一页是公开的, 可以直接访问
r = request.get(url, headers=header, data=data)
html_pages.append(r.text)

text = html_pages[0]
# 通过 regex 去获取 raw HTML 里含有的密钥
key = re.search(r'name="tempReportKey"  value="(\w+)"', text).group(1)

data["tempReportKey"] = key
data["page.PageNo"] = 2
# 注意 post 方法
html_pages.append(request.post(url, headers=header, data=data))

未按照正确方式请求会返回第一页的内容. 临时的 key 需要每次更新, 于是我们可以写出下面的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
html_pages = []
key = None

for i in range(1,4):
    from_data = {
            'page.pageNo' : i,
            'tempReportKey' : key,
            }
    if i == 1:
        r = requests.get(url, headers=headers)
    else:
        r = requests.post(url, headers=headers, data=from_data)
    text = r.text
    key = re.search(r'name="tempReportKey"  value="(\w+)"', text).group(1)
    html_pages.append(text)

提取信息

获取了原始页面之后, 我们可以利用 regex 或者 BeautifulSoup 进行文本上的提取, 来得到我们期望的数据.

  • regex 的 pattern 可能写起来比较困难, 但是它很强大
  • bs4 写起来更 friendly 一些

HTML 的基础结构是标签(tag). 例如 <b class="boldest">Extremely bold</b> 就是一个 tag. 本例中

  • b 是 name
  • class 是 attributes 中的其一
  • Extremely bold 是这个 tag 的 string, 也称 NavigableString

搜索方法比较常用的有 find_all 和 select. 例如查找所有的 <b> 标签可以这么做

1
soup.find_all('b')

也支持传入 regex. 下面这个例子是找到全部的首字母为 b 的标签, 例如 <b> 和 <body>

1
soup.find_all(re.compile('^b'))

keyword 参数查找, 用的比较多的是 href, 来找超链接

1
2
# 找到所有超链接里含 elsie 的 tag
soup.find_all('a', href=re.compile('elsie'))

如果一些 tag 属性不能作为参数名, 可以写成下面这样

1
soup.find_all(attrs={'data-foo':'value'})

我们用上面的查找 tempReportKey 的一个例子来说明:

1
2
3
4
5
# BeautifulSoup 类似于一个 parser
soup = BeautifulSoup(text, 'html.parser')
# 找到对应元素
tag = soup.find('input', {'name': 'tempReportKey'})
key = tag.get('value')

提取表单内的数据, 并将其 json 化

1
2
3
4
5
6
7
8
9
10
11
12
13
import json

pattern0 = r'<td title="(.*?)"'
results = []

for response in responses:
    results.extend(re.findall(pattern0, response))
info = []
for i in range(0, len(results), 7):
    info.append({'省/直辖市': results[i], '地市': results[i+1], '许可证编号': results[i+2], \
                 '单位名称': results[i+3], '行业类别': results[i+4], '有效期限': results[i+5], '发证日期': results[i+6]})
info_json = json.dumps(info, ensure_ascii=False, sort_keys=True, indent=4, separators=(',', ': '))
print(info_json)

数据清理

什么是数据清理? 如果已有数据存在缺省, 类型不准确, 重复等的情况, 直接把数据喂给我们的 AI 模型就印证了一句话: Garbage in, garbage out.

我们会使用 Pandas 进行方便的数据预处理.

使用的数据结构

从 Series 开始

  • 是一个带索引的数组
  • 类似 enumerate(data)

创建 DataFrame

  • 把多个 Series 拼在一起
    • 字典的键表示列名, 然后跟对应的 Series
  • 得到一个表
1
2
3
apples = Series([3,2,0,1])
oranges = Series([0,3,7,2,9,8])
fruit = DataFrame({"apples" : apples, "orange" : oranges})

切片操作: iloc(:,:)

  • 前面的是行数
  • 后面的是列数
  • 左闭右开

从 csv 文件读数据

1
trade_sh = pd.read_csv("000001_trade.csv")

对 DataFrame 的操作

很多操作和数据库查询操作很类似

  • trade_sh.head() 读取头部的(默认前五个)数据
    • 同理有 tail
  • trade_sh_2.values() 读数据

聚合操作

  • 例如 trade_sh_2.mean(axis = 0)
    • 每一列都进行取平均值操作
    • trade_sh_2.Close.mean() 指定是 Close 列

生成新的列

1
2
3
4
5
6
7
8
# 生成新的列
trade_sh_2["gap_high_low"] = trade_sh_2["High"] - trade_sh_2["Low"]
# 求这一列的最大值
max_gap = trade_sh_2.gap_high_low.max()
# 布尔值切片
boolean_slice = (trade_sh_2["gap_high_low"] == max_gap)
# 根据最大值查询
trade_sh_2[boolean_slice].index

数据类型转换

  • NaN 是字符串而不是 float
  • 2010-8-12 是字符串而不是 DateTime
  • 你去查看 dtypes 这些字符串都会被当成 object

所以你要多做一步数据转换:

  • comments["date"] = pd.to_datetime(comments.date)

删除行/列

1
2
3
4
# axis = 0表示沿着每一列或行标签\索引值向下执行
# axis = 1表示沿着每一行或列标签\索引值横向执行对应

comments.drop("url",axis = 1).head()
  • 这时候再来查看 comments 你会发现...
    • 没变动啊, DROP 掉了空气?
  • DROP 是很危险的操作.
    • 逝一世 DROP ALL DATABASES;
  • 所以上面的会复制一个 comments, 然后把 drop 后的结果返回过来.
  • 所以你要"就地"操作
    • 带一个 inplace 参数

一个删除的例子:

1
2
# 先 check 一下作者的分布
comments.author.value_counts().head()
1
2
3
4
5
6
7
author
光线传媒资讯         3782
可乐与白开水5783     2020
股神9818          519
hhl10160012     511
锅包肉1979         477
Name: count, dtype: int64

我们尤其想要知道公司自己发布的评论, 那么可以单独提取出来.

如果想分析投资人的信息, 而不关注公司的消息, 我们可以对 comments 进行一步重新赋值

1
comments = comments[comments["author"]!="光线传媒资讯"]

用 Pandas 进行文本处理

1
2
3
4
5
imdb = pd.read_table(
        'imdb_top_10000.txt',
        names=['imdbID', 'title', 'year', 'score',
               'votes', 'runtime', 'genres']
        )
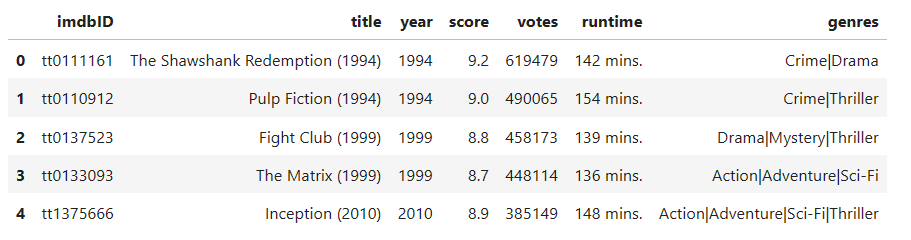
table

获取到的 Genres 里带有 | 的分割符, 我们希望把 genres 变为一个序列, 那么

1
imdb.genres.str.split("|").head()
1
2
genres = imdb.genres.str.get_dummies(sep="|") ## 哑变量生成方法，把某一列拆开
genres.head()
1
2
3
# The two dataframes can be joined according to the direction of the column
new_imdb = pd.concat([imdb,genres],axis=1)
new_imdb.head()

清理文本

  • raw data 不能拿来直接用
    • 会有前导/未导的空格
    • 会带有很多未转义的字符 \n\r
1
2
3
4
5
# remove returns
clean_comments = clean_comments.str.replace('\r\n', '')
clean_comments = clean_comments.str.replace('\r', '')

comments["comment"] = clean_comments
  • 一些评论可能带有一些 html 元素
  • 也得看网站是怎么实现评论系统的
    • 例如插入图片, 或者会有一些超链接
  • 拿 regex 清理掉
1
2
3
4
5
pattern_html = r'<.*?>'
pattern_javascript = r'{.*?}' # 这里比较简单地去掉函数体部分的代码
comments["comment"] = comments.comment.str.replace(pattern_html,"")
comments["comment"] = comments.comment.str.replace(pattern_javascript,"") # 正则表达式与字符串处理结合
comments.comment[129831]
  • 垃圾评论
    • 从别的地方 ctrl+c/v 搞来了一堆内容
    • 可能对我们的 model 是 toxic 的
  • 用 quantile 分位数 去查看评论的大致情况
1
2
print("25th percentile: ", comments.comment.str.len().quantile(0.5))
print("90%: ", comments.comment.str.len().quantile(0.9))
1
2
3
4
5
# Gets the index for comments longer than 1000 words
drop_index = comments[comments.comment.str.len()>1000].index # 布尔型索引

# drop the comments longer than 1000 words
comments.drop(drop_index,axis = 0,inplace=True) # 删除对应的行

时间处理

1
2
3
4
5
6
7
8
# 调用 Timestamp() 创建任意时间点
>>> fool_day = pd.Timestamp('2023-4-1')
>>> now = pd.Timestamp.now()
# Timestamp 相减可以获得 Timedelta 对象
>>> td = now - fool_day
# 通过 days 获得相差的天数
>>> td
Timedelta('226 days 14:45:25.988284')
1
2
3
4
5
6
# 也可以自己定义一个 Timedelta 对象
now = pd.Timestamp.now()
print(now)
td = pd.Timedelta("10 day")
now_plus_tendays = now + td
print(now_plus_tendays)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def modify_date(date_time):
    """
    调整日期，我国股市3点停盘。每天下午3点之后的评论调整为下一天的

    参数：
        date_time:评论的真实日期
    返回：
        date:调整后的日期
    """
    h = date_time.hour
    y = date_time.year
    m = date_time.month
    d = date_time.day
    date = pd.Timestamp(y,m,d)
    if h >= 15:
        date = date + pd.Timedelta("1 day")
    return date
  • 用 apply 或者 map(builtin) 就可以对一个列应用我们上面写好的自定义函数
1
2
comments["modified_date"] = comments["date"].apply(modify_date)
comments.head(10)

提取日期的特征

1
2
3
4
# 提取 hour(24个小时时刻)
comments["hour"] = comments.date.dt.hour
# 去重
comments["hour"].unique()
1
2
3
4
# 提取 dayofweek:
# 注意: 在这里 Monday=0, Sunday=6
comments["dayofweek"] = comments.modified_date.dt.dayofweek + 1
comments.dayofweek.unique()
1
2
3
# 提取month
comments["month"] = comments.modified_date.dt.month
comments["month"].unique()

保存清理好的数据

1
2
3
4
5
# 按列切片多个列
saved_comments = comments[["modified_date","comment","hour","dayofweek","month"]]

# 按日期排序后保存到 preprocessed_300251_comments.csv
saved_comments.sort_values(["modified_date"]).to_csv("cleaned_300251_comments.csv")

特征工程

创建更优秀的特征维度

机器学习基础

线性回归

导入

高中数学你就学过. 给定一组数据, 需要让你求一个回归方程 \(\hat{y}=\hat{b}x+\hat{a}\).

  • 所谓线性回归(Linear Regression), 类似于求一个线性拟合的函数.
    • 让给出的数据点尽可能靠近我们求出的直线.
  • y hat 表示一个预测的值.

人性化的题目都会给出斜率和截距的公式

\[\hat{b}=\frac{\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}, \hat{a}=\overline{y}-\hat{b}\overline{x}\]

问题是: 这些参数的公式是怎么推导出来的? 为什么这么算是对的? 当时作为高中牲的你, 也只能把它当成一个黑盒——毕竟不要求掌握——反正照着算就完事了.

我们高中接触的是一元回归问题. 自然有多元回归问题. 最常见的一个例子就是房价预测: 房价可能受房子状态, 地段, 市场行情等多种因素影响, 但我们假定这些因素对房价都是线性相关的, 因此它依然是线性回归问题.

\[\hat{\boldsymbol{y}}=\boldsymbol{Xw}+b\]

  • 假定样本量为 \(n\), 那么 \(\hat{\boldsymbol{y}}\in \mathbb{R}^{n \times 1}\), \(n\) 个输出构成的一个列向量.
  • 每一种因素, \(x^{(i)}\) 称为特征. 假定特征数为 \(d\), 那么 \(\boldsymbol{X}\in\mathbb{R}^{n\times d}\).
  • 我们希望求出模型中的参数 \(\boldsymbol{w}\) 和 \(b\)

求出模型参数的过程称为模型训练. 大体思路是: 我们先随便给出一组参数, 计算出模型的预测结果, 以及它和真实值之间的差距, 通过不断优化迭代, 最小化这个误差.

定义误差函数, 来量化误差值. 一般来说, 误差函数的值为正, 这样函数值越小, 误差也就越小. 一种想法是绝对值函数 \(\varepsilon^{(i)}=|\hat{y}^{(i)}-y^{(i)}|\), 但更常用的是平方函数(也叫能量函数)

\[\varepsilon^{(i)}=\frac{1}{2}(y^{(i)}-\hat{y}^{(i)})^2\]

求导后的常数项系数为 1, 在形式上会更简单些.

通常, 我们用训练数据集中所有样本误差的平均来衡量模型预测的质量

\[\ell(w_1,w_2,b)=\frac1n\sum_{i=1}^n\ell^{(i)}(w_1,w_2,b)=\frac1n\sum_{i=1}^n\frac12\left(x_1^{(i)}w_1+x_2^{(i)}w_2+b-y^{(i)}\right)^2\]

写成矢量形式就是

\[\ell(\boldsymbol{\theta})=\frac1{2n}(\boldsymbol{\hat{y}}-\boldsymbol{y})^\top(\boldsymbol{\hat{y}}-\boldsymbol{y})\]

其中 \(\boldsymbol{\theta}\) 表示模型参数, 即 \([w_1, w_2, b]^T\).

这样, 我们的任务就是求出模型参数 \(\mathbf{w}, b\), 使得训练样本平均损失最小.

\[w_1^*,w_2^*,b^*=\underset{w_1,w_2,b}{\operatorname*{argmin}}\ell(w_1,w_2,b).\]

Remark: 尽可能使用矢量进行运算. 例如, 两个矢量相加, 一种实现是按元素逐一相加, 但效率显然不及相关库内置的加法运算快. 此外, 类似的矢量运算也是如此, 甚至有些在硬件层面上会有优化支持.

1
2
3
4
5
6
7
8
9
10
from mxnet import nd

a = nd.ones(shape=1000)
b = nd.ones(shape=1000)
# much much slower ...
c = nd.zeros(shape=1000)
for i in range(1000):
    c[i] = a[i] + b[i]
# try this!
d = a + b

优化算法

当模型和损失函数形式较为简单的时候, 上面误差最小化的问题解可以用公式表达. 当然, 得出解析解(analytical solution) 再好不过, 但是现实情况里, 大部分的深度学习模型只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值, 得出一个数值解 (numerical solution).

求数值解的一种常用方式称为小批量随机梯度下降 (mini-batch stochastic gradient descent)

  • 随机选取一组模型参数的初始值
  • 对参数多次迭代, 每次迭代都尽可能降低损失函数的值

每次迭代过程中:

  • 随机均匀取样一个固定训练数据样本组成的小批量 (mini-batch) \(\mathcal{B}\)
  • 求小批量中数据样本的平均损失有关模型参数的梯度(导数)
  • 用它再乘上一个预先设定好的系数作为本次迭代的减小量

上面的例子里, 以 \(w_1\) 为例, 每次进行如下迭代

\[w_1\leftarrow w_1-\frac\eta{|\mathcal{B}|}\sum_{i\in\mathcal{B}}\frac{\partial\ell^{(i)}(w_1,w_2,b)}{\partial w_1}=w_1-\frac\eta{|\mathcal{B}|}\sum_{i\in\mathcal{B}}x_1^{(i)}\left(x_1^{(i)}w_1+x_2^{(i)}w_2+b-y^{(i)}\right)\]

这里 \(|\mathcal{B}|\) 表示小批量中的样本个数(批量大小, batch size), \(\eta\) 称为学习速率(learning rate). 这两个参数是预先设定的, 并非模型训练得到的, 因此称为超参数(hyperparameter).

写成矢量形式

\[\theta\leftarrow\theta-\frac\eta{|\mathcal{B}|}\sum_{i\in\mathcal{B}}\nabla_{\boldsymbol{\theta}}\ell^{(i)}(\boldsymbol{\theta})\]

其中梯度是损失有关 3 个为标量的模型参数的偏导数组成的向量.

我们下面来讨论梯度下降的具体原理.

梯度下降

我们首先以一维梯度下降为例: 假设一个关于权重的一维函数 \(\mathbb{R}\to \mathbb{R}:f(w)=w^2\), 我们知道, \(w=0\) 是损失函数的最佳参数, 我们来看看梯度下降算法是怎样趋近这个点的.

给定足够小的正数 \(\varepsilon > 0\), 根据 Taylor 展开, 可得

\[f(x+\varepsilon) \approx f(x) + \varepsilon f'(x)\]

找到 \(\eta > 0\), 使得 \(|\eta f'(x)|\) 足够小, 那么可以替换 \(\varepsilon\), 得到

\[f(x-\eta f'(x))\approx f(x)-\eta f'(x)^2\leqslant f(x)\]

这意味着, 如果我们通过

\[w\leftarrow w - n f'(w)\]

来迭代 \(w\), \(f(w)\) 的值可能会降低. 所以梯度下降就是: 从一个初始的参数, 沿着函数下降的方向逐步更新参数.

我们从 \(x=10\) 作为初始值, 设置学习率为 0.2, 使用梯度下降对 \(x\) 迭代 10 次, 可以看出 \(x\) 最终的值是接近最优解的.

1
2
3
4
5
6
7
8
9
10
11
def gd(eta):
    x = 10
    results = [x]
    for i in range(10):
        x = x - eta * 2 * x
        results.append(x)
    print('epoch 10, x:', x)
    return results

res = gd(0.1)
res
1
2
3
4
5
6
7
8
9
10
11
12
epoch 10, x: 1.0737418240000003
[10,
 8.0,
 6.4,
 5.12,
 4.096,
 3.2768,
 2.62144,
 2.0971520000000003,
 1.6777216000000004,
 1.3421772800000003,
 1.0737418240000003]

可以关注 \(x\) 的迭代的轨迹

1
2
3
4
5
6
7
8
9
def show_trace(res):
    n = max(abs(min(res)), abs(max(res)), 10)
    f_line = np.arange(-n, n, 0.1)
    plt.plot(f_line, [x * x for x in f_line])
    plt.plot(res, [x * x for x in res], '-o')
    plt.xlabel('x')
    plt.ylabel('f(x)')

show_trace(res)
x 的轨迹

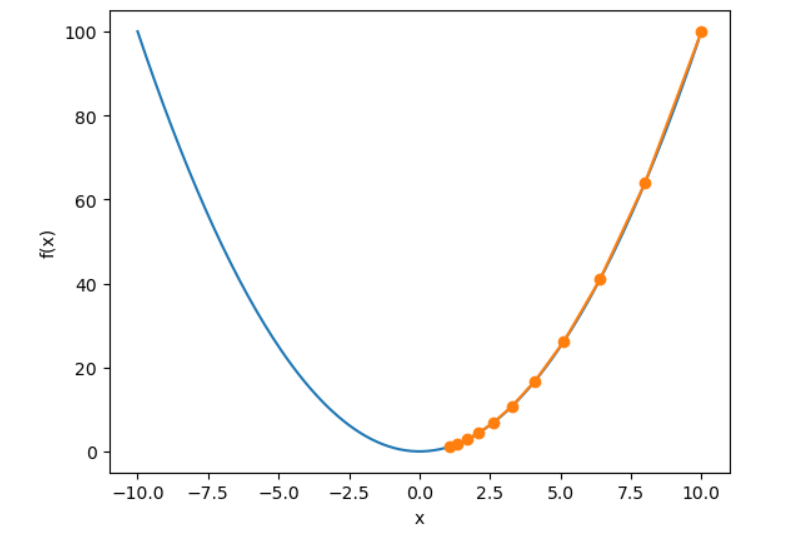
对于多维函数, 也是类似的(推导我们从略):

\[\boldsymbol{x}\leftarrow\boldsymbol{x}-\eta\nabla f(\boldsymbol{x})\]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def train_2d(trainer):
    x1, x2, s1, s2 = -5, -2, 0, 0
    results = [(x1, x2)]
    for i in range(20):
        x1, x2, s1, s2 = trainer(x1, x2, s1, s2)
        results.append((x1, x2))
    print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
    return results

def show_trace_2d(f, results):
    plt.plot(*zip(*results), '-o', color='#ff7f0e')
    x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
    plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
    plt.xlabel('x1')
    plt.ylabel('x2')
1
2
3
4
5
6
7
8
9
eta = 0.1

def f_2d(x1, x2):  # 目标函数
    return x1 ** 2 + 2 * x2 ** 2

def gd_2d(x1, x2, s1, s2):
    return (x1 - eta * 2 * x1, x2 - eta * 4 * x2, 0, 0)

show_trace_2d(f_2d, train_2d(gd_2d))
1
epoch 20, x1 -0.057646, x2 -0.000073
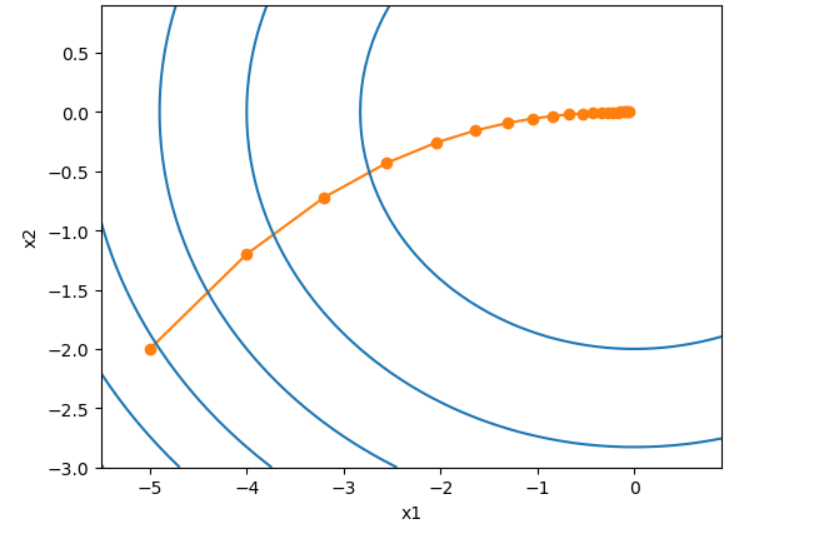
多维梯度下降

上面我们提到, 深度学习里的目标函数通常定义为各个样本的损失函数的平均.

\[f(\boldsymbol{x})=\frac1n\sum_{i-1}^nf_i(\boldsymbol{x})\]

使用全样本梯度下降, 每次自变量迭代的计算开销是 \(O(n)\). 当训练数据样本数很大时, 全样本梯度下降的计算开销很高.

随机梯度下降(stochastic gradient descent, SGD)减少了每次迭代的计算开销. 在随机梯度下降的每次迭代中, 我们随机均匀采样的一个样本索引 \(i\), 来迭代 \(x\). 可以看出, 随机梯度是对梯度的一个良好的估计.

\[x\leftarrow x-\eta\nabla f_{i}(x)\]

最常用的还属我们上面介绍的小批量随机梯度下降. 可以看出, 当 \(|\mathcal{B}|=1\) 时, 就是上面介绍的随机梯度下降; 当 \(|\mathcal{B}|=n\) 时, 就是全样本梯度下降.

线性回归实例: 房价预测

评价指标

常用模型

贝叶斯模型

也称贝叶斯分类

贝叶斯公式: 在已知一些条件下, 某事件的发生概率

\[P(A\mid B)=\frac{P(A)P(B\mid A)}{P(B)}\]

  • 条件概率(后验概率): 在 B 条件下 A 的概率 \(P(A\mid B)\)
  • 边缘概率(先验概率): 某个事件发生的概率, \(P(A), P(B)\)

推广的写法

\[P(Y=c_{k}\mid X=x)=\frac{P(X=x\mid Y=c_{k})P(Y=c_{k})}{\sum_{k}P(X=x\mid Y=c_{k})P(Y=c_{k})}\]

  • \(x\) 表示特征向量, features
  • \(y\) 表示类标记, class label, category

贝叶斯公式要求条件概率的独立性. 朴素贝叶斯法就对条件进行了独立性的假设. 也即

\[ \begin{aligned} P(X=x\mid Y=c_{k})& =P(X^{(1)}=x^{(1)},\cdots,X^{(n)}=x^{(n)}\mid Y=c_{k}) \\ &=\prod_{j=1}^{n}P(X^{(j)}=x^{(j)}\mid Y=c_{k}) \end{aligned} \]

贝叶斯模型是一种生成模型. 因为它学习的是一种生成数据的机制.

注意到贝叶斯公式中的分母对每一个 \(c_k\) 都是相同的, 于是我们只需要考虑分子的取值.

假设我们的训练数据 \(T={(x_1,y_1),(x_2,y_2),...(x_n,y_n)}\), 给定一个样本 \(x\), 我们对于每个 \(c_k\), 计算后验概率的式子

\[P(Y=c_k)\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k);k=1,2,...,K\]

最后找出后验概率最大值对应的分类, 就是

\[y=\underset{c_k}{\operatorname{argmax}}P(Y=c_k)\prod_{j=1}^nP(X^{(j)}=x^{(j)}|Y=c_k)\]

高斯朴素贝叶斯

Gaussian NB

用正态分布进行参数估计

\[P(x_i \mid y) = \frac{1}{\sqrt{2\pi\sigma^2_y}} \exp\left(-\frac{(x_i - \mu_y)^2}{2\sigma^2_y}\right)\]

1
2
3
4
5
6
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

X, y = load_iris(return_X_y=True)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
1
2
3
4
5
6
7
from sklearn.naive_bayes import GaussianNB

bnb = GaussianNB()
# 拟合模型, 然后预测
y_pred = bnb.fit(X_train, y_train).predict(X_test)

print("Number of mislabeled points out of a total {0} points : {1}".format(X_test.shape[0], (y_test != y_pred).sum()))
1
2
import matplotlib.pyplot as plt
plt.scatter(X_test[:,2],X_test[:,3],c=y_test,s=50) # 拿出两个特征, 进行可视化
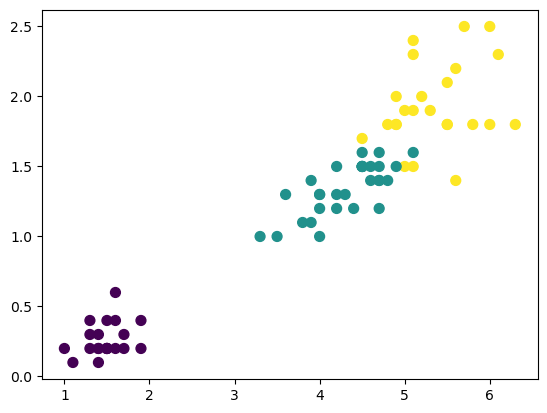
朴素贝叶斯 
1
2
from sklearn.metrics import accuracy_score
accuracy_score(y_test,y_pred)

多项式朴素贝叶斯分类器

适合离散的特征, 例如词计数的文本分类

预测: $m_j = $ "下周，持续买进，买进！" 是正面评论还是负面评论

多项式朴素贝叶斯 Multinomial NB

设每次实验结果有 \(k\) 种可能的结果, \(X_1,X_2,…,X_k\), 每种结果发生的概率分别为 \(p_1,p_2,\dots,p_k\). 进行 \(n\) 次实验, \(X_1\) 共发生 \(x_1\) 次, \(X_2\) 共发生 \(x_2\) 次, \(\dots\), \(X_k\) 共发生 \(x_k\) 次的概率为（联合概率分布）:

\[f(X_1=x_1,X_2=x_2,\cdots,X_k=x_k)=\frac{n!}{x_1!x_2!\cdots x_k!}p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k}\]

文本单词出现次数也可以看做是一种词汇多项式分布, 可能的结果是词汇表, 写一条评论可以看做是做 \(n\) 次试验 (\(n\) 表示评论中词汇的个数).

\(n(m_j,w_k)\) 表示词 \(w_k\) 在评论 \(m_j\) 中出现的次数, \(n(m_j)\) 表示 \(m_j\) 中出现的词的总数(包括重复词), \(D\) 表示词汇的总数.

\[n(m_j)=\sum_{k=1}^{D}{n(m_j,w_k)}\]

那么词汇 \(w_k\) 出现在\(c_k\)类型评论的概率

\[p(c_i,w_k) = \frac {\sum_{m_j \in c_i} {n(m_j,w_k)}}{\sum_{m_j \in c_i} {\sum_{k}n(m_j,w_k)}} = \frac {n(c_i,w_k)}{n(c_i)}\]

  • 后续要计算概率相乘, 为了避免 \(p(c_i,w_k) = 0\), 考虑 Laplace 平滑调整

\[p(c_i,w_k) = \frac{n(c_i,w_k)+1}{n(c_i)+D}\]

那么 \(c_i\) 中出现 \(m_j\) 的概率

\[P(m_j|c_i) = \frac{n(m_j)!}{\prod_{k=1}^{D}{n(m_j,w_k)!}} \prod_{k=1}^D {p(c_i,w_k)^{n(m_j,w_k)}} \]

实例: 股吧评论情感分析

调包时间到

导入数据

1
2
3
4
import pandas as pd
labeled_comments = pd.read_csv("labeled_reviews.csv",
                                index_col=False,
                                usecols= ["comment","sentiment_label"],encoding = "gbk")

对评论标注, 方法是预先分词, 根据情感词是正向多还是负向多决定它是正样本还是负样本.

数据清理

1
2
3
4
5
6
7
# 去掉 labeled_comments 中含有 "光线传媒:" 的评论
# 这些评论通常是企业自己发的
drop_index = labeled_comments[labeled_comments.comment.str.contains("光线传媒:")].index
labeled_comments.drop(drop_index,inplace=True,axis=0)
# 去掉 labeled_comments 中评论字数超过 1000 的评论评论
drop_index = labeled_comments[labeled_comments.comment.str.len()>1000].index
labeled_comments.drop(drop_index,inplace=True,axis=0)

切词工具

1
2
3
4
5
6
7
8
9
10
11
12
13
import jieba
jieba.load_userdict("userdict.txt")
def cut_comment(comment_text):
    """
    对一个段文本切词，并返回空格拼接后的字符串
    参数：
        comment_text：要被切词的股评文本
    返回：
        使用空格拼接后的字符串
    """
    r = jieba.lcut(comment_text)
    joined_text = " ".join(r)
    return joined_text
1
2
labeled_comments["cutted_comment"] = labeled_comments.comment.apply(cut_comment)
labeled_comments.tail()
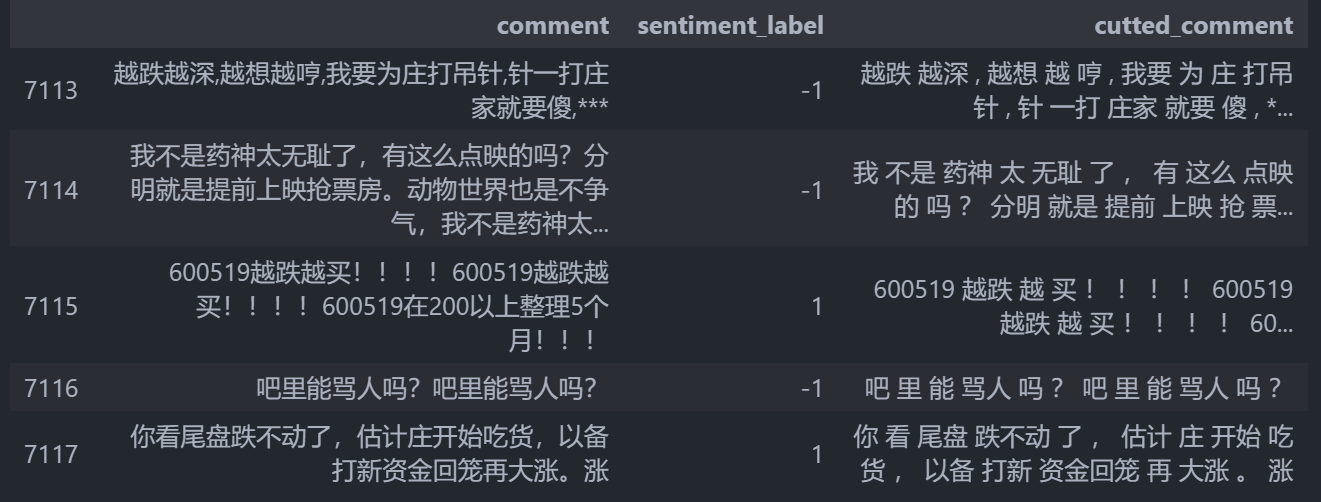
切词后的结果

生成训练集

1
2
3
4
5
6
7
from sklearn.model_selection import train_test_split
# test_size: represent the proportion of the dataset to include in the test split
# random_state: the seed used by the random number generator
X_train, X_test, y_train, y_test = train_test_split(labeled_comments.cutted_comment,
                                                    labeled_comments.sentiment_label,
                                                    test_size = 0.1,
                                                    random_state = 42)

用 CountVectorizer 去提取特征词

1
2
3
4
5
6
7
8
from sklearn.feature_extraction.text import CountVectorizer
counter = CountVectorizer(token_pattern ='\w+')
# 测试一下CountVectorizer
data = counter.fit_transform(X_train)
data = data.toarray()
columns = counter.get_feature_names_out()
term_doc_matrix = pd.DataFrame(data, columns=columns)
term_doc_matrix.head()

构建一个模型的 Pipeline

1
2
3
4
5
6
7
8
9
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import Pipeline
Multinomial_nb = MultinomialNB()

pipe = Pipeline([('count', counter), ('clf', Multinomial_nb)]) # 元组 ：名字 对象； 特征 输入到 模型里面

# 输入数据X_train.tokenized_comment, y_train训练模型

pipe.fit(X_train, y_train)
1
2
3
4
# 使用测试数据做预测,并查看准确率
from sklearn.metrics import accuracy_score
y_pred = pipe.predict(X_test)
accuracy_score(y_test,y_pred)
1
0.8388489208633093

交叉验证

1
2
3
4
5
6
# scoring: cross_val_score is similar to cross_validate but only a single metric is permitted.
from sklearn.model_selection import cross_val_score
counter = CountVectorizer()
pipe = Pipeline([('count', counter), ('clf', Multinomial_nb)])
scores = cross_val_score(pipe, labeled_comments.cutted_comment,labeled_comments.sentiment_label, cv=10,scoring="accuracy") # 10-fold 交叉验证
scores.mean()
1
0.8191089088383473

下面到了 fine-tune 环节, 首先是对输入数据的进一步清理: 我们将词袋中的停止词去掉

1
2
3
4
5
6
7
def get_Chinese_stopwords(stop_words_file):
    encoding = detect_encoding(stop_words_file)
    with open(stop_words_file,encoding = encoding) as f:
        stopwords = f.read()
    stopwords_list = stopwords.split('\n')
    custom_stopwords_list = [i for i in stopwords_list]
    return custom_stopwords_list
1
2
# https://github.com/goto456/stopwords
stop_words = get_Chinese_stopwords("stopwordsHIT.txt") # 读取停用词
1
2
3
4
5
6
7
8
counter = CountVectorizer(token_pattern ='\w+')
pipe = Pipeline([('count', counter), ('clf', Multinomial_nb)])
pipe.set_params(count__stop_words=stop_words)
# 有两个下滑线，第二个下划线表示参数

# 输入数据X_train.tokenized_comment, y_train训练模型

pipe.fit(X_train, y_train)  ## 重新拟合
1
2
3
4
#使用测试数据做预测
from sklearn.metrics import accuracy_score
y_pred = pipe.predict(X_test)
accuracy_score(y_test,y_pred)
1
0.8489208633093526

分数比之前高了一些些

生成 n-gram 词汇

n-gram 用一个滑动窗口去读取句子中连续的单词, 例如 "I love u" 生成的 bigram 单词就是 "I love", "love u".

1
2
3
4
5
6
7
counter = CountVectorizer(token_pattern ='\w+')
pipe = Pipeline([('count', counter), ('clf', Multinomial_nb)])
pipe.set_params(count__stop_words=stop_words,count__ngram_range=(1,2))

# 输入数据X_train.tokenized_comment, y_train训练模型

pipe.fit(X_train, y_train)
1
2
3
4
#使用测试数据做预测
from sklearn.metrics import accuracy_score
y_pred = pipe.predict(X_test)
accuracy_score(y_test,y_pred)
1
0.8633093525179856

交叉验证

1
2
3
4
5
6
counter = CountVectorizer(token_pattern ='\w+')
pipe = Pipeline([('count', counter), ('clf', Multinomial_nb)])
pipe.set_params(count__stop_words=stop_words,count__ngram_range=(1,2))
scores = cross_validate(pipe, labeled_comments.cutted_comment,labeled_comments.sentiment_label, cv=10,return_train_score=False,
                       scoring=("accuracy","recall","precision","f1"))
scores.get("test_accuracy").mean()

保存模型

1
2
3
4
5
6
7
# 上面的实验较为多，这里建议重新运行一下这个cell的代码，拟合模型MultinomialNB_pipe

counter = CountVectorizer(token_pattern ='\w+')
Multinomial_nb = MultinomialNB()
MultinomialNB_pipe = Pipeline([('count', counter), ('clf', Multinomial_nb)])
MultinomialNB_pipe.set_params(count__stop_words=stop_words,count__ngram_range=(1,2))
MultinomialNB_pipe.fit(X_train, y_train)
1
2
3
4
5
6
7
# 保存朴素贝叶斯模型MultinomialNB_pipe
# 参数、结果、结构进行序列化

# from sklearn.externals import joblib

import joblib
joblib.dump(MultinomialNB_pipe, "MultinomialNB_model.m") # 导出模型

支持向量机 SVM

监督学习: 在特征空间内找到超平面, 将样本分到不同的类别中

决策树/随机森林

预测模型, 分类

对特征重要性进行排序

核心: 熵理论

参考资料

  1. OReilly Hands On Machine Learning with Scikit Learn and TensorFlow 2nd, 以及它的仓库
  2. 动手学深度学习 Dive into Deep Learning
  3. 深度强化学习 王树森 黎彧君 张志华 著
  4. 校内课程资料

  1. 其实是不会跑路的. 为我的队友负责.↩︎