离散考前挣扎

发表于 更新于 分类于 本文字数： 1.6k 阅读时长 ≈ 6 分钟

考前的最后挣扎. 全是题目, 不再一五一十地复习基本概念了, 会做题和懂数学是两码事, 时间该留到平时钻研.

说实话这学期的离散学的内容还是太松散了. 数理逻辑, 关系代数, 图论, 然后没了. 我觉得这门课改成 Introduction to Discrete Mathematics 可能更合适. 隔壁 UESTC 同一本教材讲得明显比咱好, NJU 的佬问我问题一查大半天, 惭愧.

总结一下往年的试卷和作业试题. 总的来说还是很简单的. 其实我还有一个习题集, 但那个超纲很多, 说不定哪天合并一下.

数理逻辑

求主范式

求命题公式 \(G(P,Q,R)=\neg (\neg P \rightarrow Q) \vee (Q \wedge R)\) 的主合取范式和主析取范式, 求解结果用 \(m_i\) 和 \(M_i\) 的编码形式表示.

解

\[\begin{aligned} G(P,Q,R) &= \neg (P \vee Q) \vee (Q \land R) \\ &=(\neg P \land \neg Q) \vee (Q \land R) \\ &=(\neg P \land \neg Q \land \neg R) \vee (\neg P \land \neg Q \land R) \vee (\neg P \land Q \land R) \vee (P \land Q \land R)\\ &= m_0\vee m_1 \vee m_3 \vee m_7 \\ &=M_2 \wedge M_4 \wedge M_5 \wedge M_6\\ &=(P \vee \neg Q \vee R) \wedge (\neg P \vee Q \vee R) \wedge (\neg P \vee Q \vee \neg R) \wedge (\neg P \vee \neg Q \vee R) \end{aligned} \]

求前束范式

求谓词公式 \((\exists x)((\forall y)(\exists z)P(x,y,z)\to(\exists z)(\forall t)(Q(x,z)\lor R(x,t,z)))\) 的前束范式. 其前束范式和原公式之间的关系满足什么性质?

解

\[ \begin{aligned} &(\exists x)((\forall y)(\exists z)P(x,y,z)\to(\exists z)(\forall t)(Q(x,z)\lor R(x,t,z))) \\ &=(\exists x)(\neg(\forall y)(\exists z)P(x,y,z)\lor(\exists z)(\forall t)(Q(x,z)\lor R(x,t,z))) \\ &=(\exists x)((\exists y)(\forall z)\neg P(x,y,z)\lor(\exists z)(\forall t)(Q(x,z)\lor R(x,t,z))) \\ &=(\exists x)((\exists y)(\forall z)\neg P(x,y,z)\lor(\exists w)(\forall t)(Q(x,w)\lor R(x,t,w))) \\ &=(\exists x)(\exists y)(\forall z)(\exists w)(\forall t)(\neg P(x,y,z)\lor Q(x,w)\lor R(x,t,w)) \end{aligned} \]

它们是等价关系.

演绎证明

用演绎法证明下述推理的有效性:

  1. 明天下午或者是天晴，或者是下雨；仅当我去登山，明天下午才是天晴；只有我不学习，我才去登山。因此，如果我在学习，则天在下雨。

  2. 每个喜欢吃肉的人都不喜欢吃汤圆；每个人或者喜欢吃饺子或者喜欢吃汤圆；有的人不喜欢饺子。因而有的人不喜欢吃肉。

解 (1) 符号化:

  • P: 明天下午天晴
  • Q: 明天下午下雨
  • R: 明天下午登山
  • S: 明天下午学习

上述命题可以翻译为: \(P \oplus Q, P \to R,R \to \neg S\Rightarrow S \to Q\)

下面是证明:

  1. \(S \qquad \qquad \quad P(附加前提)\)

  2. \(R\to \neg S \qquad P\)

  3. \(\neg R \qquad \qquad T,1,2,I\)

  4. \(P\to R \qquad \quad P\)

  5. \(\neg P \qquad \qquad T,3,4,I\)

  6. \(P \oplus Q \qquad \qquad P\)

  7. \(Q \qquad \qquad \quad T,5,6,I\)

  8. \(S\to Q \qquad \quad CP,1,7\)

  9. 符号化:

  • \(H(x)\): \(x\) 是人
  • \(P(x)\): \(x\) 喜欢吃汤圆
  • \(Q(x)\): \(x\) 喜欢吃饺子
  • \(R(x)\): \(x\) 喜欢吃肉

翻译: \((\forall x)(H(x)\land R(x)\to \neg P(x)), (\forall x)(H(x)\to P(x) \lor Q(x)),(\exists x)(H(x)\land \neg Q(x))\Rightarrow (\exists x) (H(x)\land \neg R(x))\)

下面是证明:

  1. \((\exists x)(H(x)\land \neg Q(x)) \qquad \qquad P\)
  2. \(H(c)\land \neg Q(c) \qquad \quad \qquad \qquad ES, 1\)
  3. \(H(c) \quad \qquad \qquad \qquad \qquad \qquad T,2,I\)
  4. \(\neg Q(c) \qquad \qquad \qquad \qquad \qquad T,2,I\)
  5. \((\forall x)(H(x)\to P(x) \lor Q(x)) \qquad P\)
  6. \(H(c)\to P(c) \lor Q(c) \qquad \qquad US,5\)
  7. \(P(c) \lor Q(c) \qquad \qquad \qquad \qquad T,3,6,I\)
  8. \(P(c) \qquad \quad \qquad \qquad \qquad\qquad T,4,7,I\)
  9. \((\forall x)(H(x)\land R(x)\to \neg P(x)) \qquad P\)
  10. \(H(c)\land R(c)\to \neg P(c)\qquad \qquad US,9\)
  11. \(\neg (H(c)\land R(c)) \qquad \qquad\qquad T,8,10,I\)
  12. \(\neg H(c) \lor \neg R(c) \qquad\qquad\qquad T,11,E\)
  13. \(\neg R(c) \qquad\qquad\qquad\qquad\qquad T,3,12,I\)
  14. \(H(c)\land \neg R(c) \qquad\qquad\qquad T,3,13,I\)
  15. \((\exists x) (H(x)\land \neg R(x)) \qquad\qquad EG, 14\)

关系代数

证明关系

设 \(A=\{1,2,3,4\}\), 在 \(P(A)\) 上规定二元关系如下:

\[ R = \{ <u,v>|u,v\in P(A) \land(|u|=|v|) \} \]

  1. 证明: \(R\) 是 \(P(A)\) 上的等价关系.
  2. 写出商集 \(P(A) / R\).

解 (1) 分别证明自反, 对称, 传递性.

  • 对于 \(\forall s \in P(A)\), \(|s|=|s|\), 于是 \(<s,s>\in R\), 自反性得证.
  • 对于 \(\forall s, t \in P(A)\), \(<s,t> \in R\), 显然 \(|s|=|t|\), \(|t|=|s|\), 于是 \(<s,t>\in R, <t,s>\in R\), 对称性得证.
  • 对于 \(\forall s,t,r\in P(A)\), \(<s,t>\in R, <t,r>\in R\), 显然 \(|s|=|t|=|r|\), 于是有 \(<s,r>\in R\), 传递性得证.

因此 \(R\) 是 \(P(A)\) 上的等价关系.

  1. \(P(A)=\{\{\varnothing \},\{1\},\{1,2\},\{1,2,3\},\{1,2,3,4\}\}\)

闭包运算

设 \(A = \{a, b, w+1, \varnothing\}\), 定义 \(A\) 上的二元关系

\[ R=\{<a,b>,<b,w+1>,<w+1,\varnothing>,<\varnothing,a>\} \]

求: \(r(R), s(R)\) 以及 \(t(R)\).

解

\[r(R)=\{<a,b>,<b,w+1>,<w+1,\varnothing>,<\varnothing,a>,<a,a>,<b,b>,<w+1,w+1>,<\varnothing,\varnothing>\}\]

\[ s(R)=\{<a,b>,<b,w+1>,<w+1,\varnothing>,<\varnothing,a>, <b,a>, <w+1,b>, <\varnothing, w+1>,<a,\varnothing>\} \]

\(R\) 的关系矩阵 \(M_1=\begin{pmatrix}0&1&0&0\\ 0&0&1&0\\ 0&0&0&1\\ 1&0&0&0\end{pmatrix}\)

\(t(R)\) 的关系矩阵为 \(M=M_1\vee M_2\vee M_3\vee M_4=\begin{pmatrix}1&1&1&1\\ 1&1&1&1\\ 1&1&1&1\\ 1&1&1&1\end{pmatrix}\), 于是 \(t(R)\) 即为 \(A\times A\).

图论

距离和连通性

设有向图 \(G=<V,E>\), \(V=\{v_1,v_2,v_3, v_4\}\), 如下图所示, 回答:

图 G
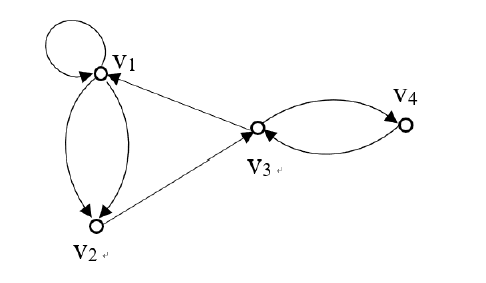
  1. 长度为 \(3\) 的路一共有几条? 其中回路有几条?
  2. 图论中, 哪类图的可达性矩阵一定是对称的? 计算 \(G\) 的可达性矩阵, 判断其是否是对称矩阵.

解 (1) 图 \(G\) 的邻接矩阵为

\[\text{A}=\begin{pmatrix}1&2&0&0\\ 0&0&1&0\\ 1&0&0&1\\ 0&0&1&0\end{pmatrix}\]

\[A^2=\begin{pmatrix}1&2&2&0\\ 1&0&0&1\\ 1&2&1&0\\ 1&0&0&1\end{pmatrix}\mathrm{A}^3=\begin{pmatrix}3&2&2&2\\ 1&2&1&0\\ 2&2&2&1\\ 1&2&1&0\end{pmatrix},\mathrm{A}^4=\begin{pmatrix}5&6&4&2\\ 2&2&2&1\\ 4&4&3&2\\ 2&2&2&1\end{pmatrix}\]

于是 \(G\) 中长度为 3 的通路有 24 条, 有 7 条回路.

  1. \(G\) 可达矩阵为 \(P=\begin{pmatrix}1&1&1&1\\ 1&1&1&1\\ 1&1&1&1\\ 1&1&1&1\end{pmatrix}\), 是一个对称矩阵.

证明题

设 \(G\) 是具有 \(k (k \geqslant 2)\) 个连通分支的平面图, 证明:

\[ n - m + r = k + 1 \]

其中 \(n,m,r\) 分别为 \(G\) 的结点数, 边数和面数.