数理逻辑人话ver

发表于 2023-03-11 更新于 2023-06-14 分类于离散数学本文字数： 6.5k 阅读时长 ≈ 24 分钟

为了严谨性以及交流方便, 我们需要术语来描述问题: 这很好, 某些问题数学语言胜千言——但由 terminology 组成的句子经常会让人不知所云. 尤其对于数理逻辑, 因为是翻译文字所以句子看起来就更糟心了. 本身不是数学专业, 还要被符号定义纠缠半死. 想要明白问题的核心要义, 非得二次翻译不可, 但最后描述的事情却是显而易见的.

It is not what you read, but how you read it.——Richard Feynman

一切在于你的理解: 是愿意如背古诗一般去背定义——事实上这也足够你做题了——还是真真正正地去理解所描述的问题? 以及, 为什么要这么定义?

命题逻辑

免责声明: 这不是教会你怎么去应试的.

你学的是 CS, 那么学数学理应把数学和 CS 紧密联系起来. 说我们学习数学是效用主义, 没错, 就要这样.

与其在脑子里装些不明不白的"定义", 倒不如对逻辑学里讨论的问题以及讨论的方法多一些认真.

这篇文章只是对数理逻辑的一个简单梳理, 忽略了许多数学上的严谨性, 某些"末节"和"小技"在应对复杂的数学问题时就体现出它应有的作用.

命题符号化

句子变符号

什么是命题(statement)? 一个布尔值.

1 + 1 != 2 false
1 + 1 = 2 (~~哈? 这不是赋值语句嘛.~~) true

换句话说就是: 有确切真值的陈述句(定义).

\(\sqrt{2}\) 是无理数. true

要求: 不能含糊不清(ambiguious).

x + 1 == 2 (x is undefined)
I love you. (Hmmm...)

所谓命题的符号化就是给命题起一个标识符. 比方说:

P = (1 == 2) (p = false)
P = 可导一定连续 (p = true)

上面的 P 就称为原子命题. 举手: 老师, 那有分子命题吗? 你猜对了. 不过我们叫它复合命题.

联接词就是连起来

联接词(connective)可以认为是连接原子命题之间的化学键.

联接词是逻辑运算符. 熟悉编程语言, 这东西再简单不过. 只不过是换成数学的符号, 多一个名字而已:

\(P\wedge Q\) 合取(conjunction) (&&, and)
- 当且仅当 \(P\) 和 \(Q\) 同为真为真.
- 把合取理解成乘法: 如果有一个零, 乘积就是零, 真值就为 0.
- P = 1 != 2, Q = 1 % 2 == 0, 那么 \(P \wedge Q = 1 \wedge 0 = 0\).
\(P\vee Q\) 析取(disjunction) (||, or)
- 当 \(P\) 和 \(Q\) 任一为真即为真.
- 把析取理解成加法: 如果有一个 1, 和就必定大于等于 1, 那么真值就为 1.
- P = 1 != 2, Q = 1 % 2 == 0, 那么 \(P \vee Q = 1 \vee 0 = 1\).

上面都是二元运算符, 联接词就是把真值连起来.

否定联接词稍微特殊一些, 它是一元的. 搞得像它应该被开除联接词籍:

\(\neg P\) 否定(negation) (!, not)
- 反转一个布尔值.
- P = 1 > 2, 那么 \(\neg P = 1\).

如果你熟悉位运算的话, 这点联接词也能说是布尔变量(之间)的 & | ! 运算. 你可能会好奇: 我异或 xor ^ 呢? 事实上, 异或其实也是有对应联接词的(\(P\oplus Q\)).

试试看你能不能只用 & 和 ! 模拟出 ^!

int bitXor(int x, int y)
{
    int p = ~((~x) & (~y)); // or
    int q = ~(x & y);
    return p & q; // Xor
}

Remark: 这个例子实际上说明了基本运算符可以剪裁. or 可以被 and 和 neg 模拟, 等价的一种说法是在 \(\{ \neg, \wedge\}\) 上构造 \(L\). (\(L = \oplus\)). 这也说明了某些真值联接词具有函数完全性, 比方说所有真值函数都可以在 \(\mathscr{L}_{\neg,\vee,\wedge}\) 中表达.

剩下两个联接词很常用. 但它们同样可以被上面三种联接词模拟出来.

\(P\rightarrow Q\) 蕴含(implication)
- \(P\) 称作假设(hypothesis), \(Q\) 为结论(conclusion). (~~前件和后件?~~ 真不熟)
- 规则: 1 ➡ 1 = 1, 1 ➡ 0 = 0, 0 ➡ 1 = 1, 0 ➡ 0 = 1
- 除了 P = true, Q = false 外其它情况都为 true.
- P 为 false 而整个蕴含式一定为真(vacuously true)¹.
\(P\leftrightarrow Q\) 等价(equivlance) (==)
- 童贞同真时为真, 同假时也为真.
- 也叫双蕴含. iff

什么蕴含? 看符号不就是推出嘛. 就是 P 可以推出 Q, 如果成立, 就为真(?).

P: 1+1=2, Q: 地球绕着太阳转
\(P \rightarrow Q\) 的含义:
C: 如果 1 + 1 = 2, 那么地球绕着太阳转.

你看规则上说的, 1 implies 1 is 1, 那么 C 也是 1. 但这句话非常令人迷惑 🤔. 两个毫不相关的事实, 然后声明"事实推事实"为真, 这是在干什么.

特别说明一点: 真值的联结不等同于命题间的联结. 牢记一点, 命题都是 1 和 0.

讨论符号和公式的理论称为语义(semantics)理论. 1 + 1 = 2 和 one plus one equals two 是同一个语义.

蕴含可能会出现各种各样的地方, 或许你意识不到:

不能玩游戏( \(\neg p\) ), 除非写完作业(unless \(q\))
不写完作业, 就不能玩游戏. (\(\neg q \rightarrow \neg q\))

下面的都等价于 \(P \rightarrow Q\):

if P, then Q
Q if P
P only if Q
P 是 Q 的充分(sufficient)条件.
Q 是 P 的必要(necessary)条件.
Q unless not P.

联接词有没有运算的优先级? 有. 要不要记? 不用. 总之按顺序算就对了.

命题表达式

我们之前提到过, 命题必须是一个确切的真值语句.

那可真可假怎么办? 也就是一个布尔变量, 0 或 1. 此时我们称其为命题变元.

用联接词, 我们可以将原子(简单)命题联系起来, 得到了复合命题. 同样, 命题变元的联结构成了一个命题表达式, 或者说是 propositional form, 或者说是 Well-Formed Formula(WFF)², 或者说是 truth-value function.

严谨起见, 命题表达式是递归定义的:

单个命题变元 \(p_1, p_2, \dots\) 是命题表达式.
如果 \(\phi\) 是命题表达式, 那么 \(\neg \phi\) 也是.
如果 \(\phi\) 和 \(\psi\) 都是命题表达式, 那么用联接词联结得到的新表达式也是.
只有有限次应用上述规则的符号串才是命题表达式.

这个定义约定了命题表达式的"语法". 现在, 你就可以写一个算法, 来判定一个字符串是否是有效的命题表达式了! (我们留作习题 :)

命题逻辑的判定

解释和真值表

给命题表达式 \(G\) 解释 \(I\) == 给所有的命题变元 \(p_1, p_2,\dots,p_n\) 赋值

别扭的说法: 做一组指派(assignment), 如果命题表达式此时为真, 则称做一组成真指派(~~全真教派~~).

命题公式所有解释下得到的真值, 构成一张表, 叫真值表(truth table). 换句话说就是枚举了所有情况然后打表.

我们给出一个例子:

P	Q	P ➡ Q
0	0	1
0	1	1
1	0	0
1	1	1

命题表达式的分类

如果打表发现所有解释下, 真值都为真, 那么这个表达式就叫永真公式, 也叫重言式(tautology). 真值全为假, 称其永假公式, 也叫矛盾式(contradiction). 不是矛盾式就是可满足式.

注意: 可满足式不是偶然式(或然式, contingency).

判定一个公式是否是永真公式, 最简单的办法就是枚举, 也就是列出真值表.

例如上面的真值表, 我们实际上证明了 \((P \rightarrow Q) \leftrightarrow (\neg P \vee Q)\) 是一个永真公式. 不信你再多看看.

有无算法, 能够判定对于一个任意的命题公式 \(\phi\), 其是否可满足? 这个问题也叫 SAT(或 3-SAT) Problem, The Satisfiability Problem.

求解: 真值表枚举, 指数级的时间复杂度. 它是 NP-Complete 问题, Cook-Levin Theorem 描述的就是这个事情. 如果你对算法分析感兴趣可以 Google 一下!

逻辑等价

如果我们能证明 \(P \leftrightarrow Q\) 是个永真公式, 那么我们称 \(P\) 和 \(Q\) 是逻辑等价的(也叫重言等价). 用符号 \(P=Q\), \(P \Leftrightarrow Q\) 或者 \(P\equiv Q\) 表示.

那么 \(\equiv\) 和 \(\leftrightarrow\) 有什么区别吗? 结论: 这里没区别. 到一阶谓词逻辑才有区别.

类似的, 你可以用打表证明德摩根律(De Morgan's Laws): Distribute and Flip

\[\neg (P \wedge Q) \equiv (\neg P \vee \neg Q)\]

\[\neg(P \vee Q) \equiv (\neg P \wedge \neg Q)\]

打表可以建立以下的 24 种基本的等价关系:

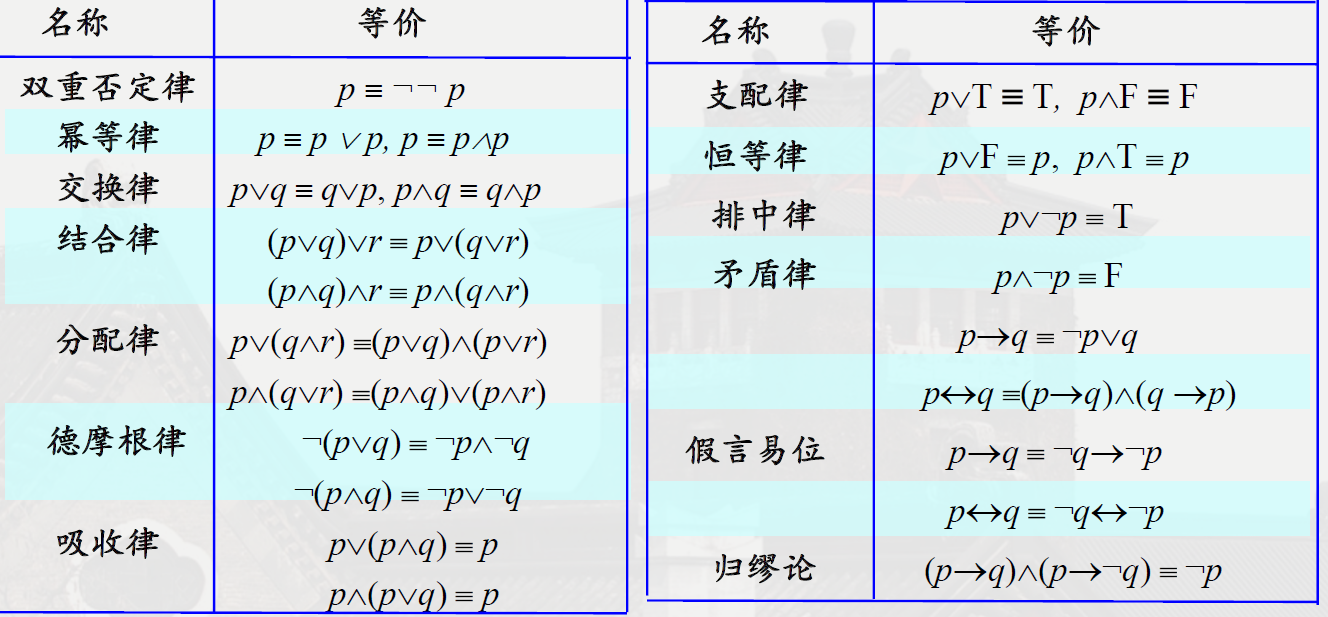
举手: 这些公式都要记吗? 要. 但实际上不难记忆, 就把联接词当成加法乘法来看待. 记住几个最常用的足足够了.

对于一个 \(n\) 元的命题表达式, 显然有 \(2^n\) 种赋值方式. 或者, 对于一个表达式很长的命题公式, 显然打表去求一个表达式的等价公式效率太低了. 此时可以用上面的这些基本等价公式去化简, 有时甚至能直接判定:

例 1 \(\neg(p \rightarrow q)\) 和 \(p \wedge \neg q\) 逻辑等价吗?

\[ \begin{aligned} \neg(p \rightarrow q) & \equiv \neg(\neg p \vee q) \\ & \equiv \neg(\neg p) \wedge \neg q \\ & \equiv p \wedge \neg q \end{aligned} \]

例 2 小明写了下面的程序

if (a) {
    if (b) {
        x();
    } else {
        y();
    }
} else {
    if (b) {
        x();
    } else {
        y();
    }
}

请你帮他改改代码.

解分析一下, 执行 \(x\) 条件是 \((a\wedge b)\vee (\neg a \wedge b) = b\), 执行 \(y\) 条件 \((a\wedge \neg b)\vee (\neg a \wedge \neg b) = \neg b\), 所以

if (b)
    x();
else
    y();

逻辑蕴含

有逻辑等价, 有逻辑蕴含吗? 有!

\(\phi\models \psi\) 定义为: 对于 \(\phi\) 任一为真的解释, \(\psi\) 为真; 换言之 \(\phi \rightarrow \psi\) 永真.

例如 \((P \rightarrow Q) \models (\neg P \vee Q)\).

此外我们定义 \(\phi\) 永真当且仅当 \(\models \phi\). (称 \(\phi\) is valid)

举手: 那么 \(\rightarrow\) 和 \(\models\) 有什么区别吗? \(\models\) 和 \(\Rightarrow\) 有什么区别吗?

我们之前提到, 联接词是一种布尔值之间的运算, 最后得到一个新的真值为 0 或 1 的命题(复合命题), 可以理解 \(\rightarrow\) 就是一个运算符, 我们关注的是运算后得到的值. 而 \(\models\) 表示的是命题之间的关联, \(P\) 推 \(Q\), 这个"推"用的就是 \(\models\); 我们关注的侧重点不是 \(\phi\models \psi\) 等于多少, 它已经永真了.

至于 \(\Rightarrow\), 平时在写数学题你会用到这个记号, 例如从条件 1 可以推出条件 2, 条件 2 推出条件 3, 直到推出结论. 那么这里的"推出"你会写 \(\Rightarrow\) 而不是数理逻辑里的符号 \(\models\). 当然, 一般来说我们也不区分 \(\Rightarrow\) 和 \(\models\), 你也可以认为这两个符号等价.

当然, 这个世界上还存在一个 \(\vdash\) 的东西. 如果你感兴趣, 你可以 check 这个回答.

规范化(canonical)

范式

什么是范式? 在回答这个问题之前, 我们需要引入一些相关的定义:

命题变元或命题变元的否定称为文字.
有限个文字的析取式称为简单析取式(基本和)
有限个文字的合取式称为简单合取式(基本积)
由有限个简单合取式构成的析取式称为析取范式.
由有限个简单析取式构成的合取式称为合取范式.

简单来说:

OR 连接 AND(称简单合取式或基本积) 的式子称为析取范式(DNF).
AND 连接 OR(称简单析取式或基本和) 的式子称为合取范式(CNF).

这么理解就好懂它的命名了:

简单合取式, 就是一堆变元³ AND 相连得到的式子. 之前讲过 \(\wedge\) 可以理解成乘法, 所以也叫做基本积.
析取范式, 那么就是 OR 相连得到的式子, 只不过基本单位是上面的基本积. 因为规范过, 所以称为范式.
剩下同理.

举几个例子就很清楚了:

\[ \begin{array}{l} (1) p \\ (2) p \vee q \vee \neg r \\ (3) \neg p \wedge q \wedge r \\ (4) (p \wedge q) \vee(\neg p \wedge q) \\ (5) (p \vee q) \wedge(\neg p \vee q) \end{array} \]

类似 (1) 这样的命题表达式(文字)既是析取范式又是合取范式. 这不是一种约定, 通过幂等律可以说明这一点.

是一个析取范式(用 or 连接). 但同时也可以看成是一个合取范式, 只需要 \((p \vee q \vee \neg r)\wedge T\) 即可.
是一个合取范式(用 or 连接). 但同时也可以看成是析取范式.
只能是一个析取范式. (5) 只能是一个合取范式.

定理任何命题公式可以化成析取范式或合取范式的形式, 而且二者(重言)等价.

我们的操作如下:

首先用等价公式消去 \(\rightarrow\) 和 \(\leftrightarrow\).
消去多余的 \(\neg\).
用分配律化成 DNF 或 CNF.

主范式

DNF 和 CNF 实际上不唯一. 例如 \(P \wedge (Q \vee R)\) 还可以写成 \((P \vee P) \wedge (Q \vee R)\) 之类.

范式还不够强, 要进一步约束限定, 于是就有了主范式. 主范式规定的是它的基本构成:

对于合取范式中的每一个简单析取式, 要求包含所有的命题变元, 且每个只能出现一次.(称其为极大项, maxterm)
- 主合取范式就是由有限个极大项组成的布尔表达式.
对于析取范式也是如此. 简单合取式更名为了极小项(minterm).

举个例子:

对于三个变元的场景, \(P \wedge Q\) 不是极大项, 因为还缺了一个变元.
只考虑两个变元: \(P \wedge \neg P\) 不是极大项, 因为 \(P\) 变元出现了两次. (显然出现两次同一个变元, 合取是永假的)
\(P \wedge Q\) 是一个极大项, 每一个变元前可以加一个 \(\neg\), 所以对于只有两个变元的情况, 极大项有 4 个, 极小项也有 4 个.

容易推广, 对于 \(n\) 个命题变元, 可以组合出 \(2^n\) 个极大项和 \(2^n\) 个极小项.

为什么称规范后的简单析取式为极大项? 一种解释是, 析取是对所有变元(或变元的否)取极大值:

\[p_1 \vee p_2 \vee ... \vee p_n = \max \{p_1, p_2, ..., p_n \}\]

观察到一个性质: 全体极大项的合取永假(总存在唯一的一个假的极大项), 全体极小项的析取永真(总存在唯一的一个真的极小项).

这其实很好理解: 当且仅当所有变元为假时, 简单析取式为假; 当且仅当所有变元为真时, 简单合取式为真.

利用唯一性, 我们可以对极小项和极大项编码. 我们用 \(1\) 表示一个命题变元, \(0\) 表示命题变元的否, 这么做恰好能满足编码的完备性, 对于极小项:

\(P \wedge Q \wedge \neg R\) 就可以编码成 \(110\), 用 \(m_{110}(m_6)\) 表示.

对应的真值表上的一组成真赋值:

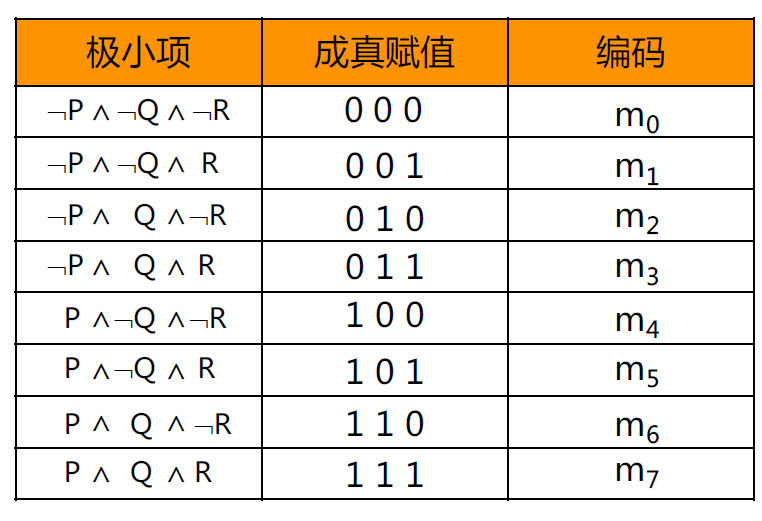
对于极大项, 那么就是按照成假赋值去编码. 例如 \(P \vee Q \vee \neg R\) 就是 \(001\), 也就是 \(M_{001}(M_1)\).

编码计算思维的体现: 假设 \(B = \{0, 1\}\), \(B^{A}\) 表示 \(A\) 到 \(B\) 的所有函数构成的集合, 那么 \(B^A = P(A)\), 通常也记 \(2^{A}\), 我们可以用类似编码的思想来说明!

显然, 没有两个不同的极大项(极小项同理)是等价的. 那么极大项的组合(极小项同理)也是唯一的. 这样规范以后, 就保证了范式的唯一性.

这实际上表示了一种 \(B^{n}\to B\) 的一种映射关系(函数).

在求出了主合取范式了以后, 它的主析取范式也就确定了. 反之亦然. 我们可以简单推导一下: 假设主合取范式为 \(G\), 那么

\[G = \vee^{k}_{i = 1} M_{l_i}\]

对应主析取范式 \(G=\neg(\neg G)=\neg (\vee^{2^{n}-k}_{i = 1} M_{l_i})=\vee^{2^{n}-k}_{i=1}(\neg M_{l_i})=\vee^{2^{n}-k}_{i=1}m_{l_i}\).

用真值表就很清楚了. 动手试试看!

最终任务: 推理

数理逻辑的最大作用: 把推理形式化.

什么是推理? 举一个简单的例子:

前提: 1. 如果天下雨, 那么路上有水. 2. 天下雨了结论: 路上有水

简单的符号化: 如果 A, A->B, 那么 B.

A: 下雨
B: 路上有水

这就是一个有效(valid)推理(或者说这个论说是好的). 这里前提(premises)是 A 和 A->B, 结论(conclusion)为 B.

所谓有效推理, 并不要求我们的前提和结论一定为真. 若前提为真, 则结论为真, 这就合乎逻辑.

有一个误区是:"你的前提是假的, 即便论说是有效的, 但结论一定是假的". 例如你怎能确定今天一定下雨? 如果不下雨, 路上就没有水, 结论明显为假, 你的论证不对.

我们可以举出一个反例:

前提: 1. 所有的猫都是人. 2. 所有的学生都是猫结论: 所有的学生都是人

两个前提都是假的, 但结论无疑是真的. 此时你可能会开始质疑, 是这个论证的问题吗? 换句话说, 怎么去说明一个论证是坏的?

如果一个论说的形式存在反例(counterexample), 那么他就是坏的. 例如:

前提: 1. 企鹅都是鸟 2. 猴子都不是企鹅结论: 猴子都不是鸟

考虑反例:

前提: 1. 企鹅都是鸟 2. 麻雀都不是企鹅结论: 麻雀都不是鸟

显然两个前提为真, 但结论为假. 这明显和上面的例子矛盾! 这个论说是不满足一致性(consistency)的, 或者说不自洽的. 这个例子, 和上面的例子, 都是一个无效的论证.

回到上例, 如果今天没下雨, 显然天下雨了这个前提不成立, 但这影响这个推理的有效性吗?

"今天下雨"的情况取决于实际情况, 也就是需要一个解释. 我们的推理如果有效, 对于任意的解释, 都成立. 这里的成立指的是

在我们的符号化中, 我们实际上要说明的是 \(A \wedge (A\rightarrow B)\rightarrow B\) 在任何解释 \(I\) 下都为真, 也即, 它是个永真公式, 也即 \(A \wedge (A\rightarrow B)\Rightarrow B\) (条件 \(\Gamma\) 逻辑蕴含 \(H\))

这就是我们推理有效的理论支撑!

进一步推广, \(\Gamma\) 是一组前提构成的集合, 这些前提的合取可以推出 \(H\). 我们验证一个推理是否有效, 只要证明 \(G_1\wedge G_2\wedge...\wedge G_n\rightarrow H\) 永真即可! 不过, 正如我们上面所叙述的, 判断永真公式是个 NP hard 的问题, 我们需要一种更有效的推理方法, 这就引出了演绎法.

基于规则的推理: 演绎法

命题逻辑有不同的演绎系统, 例如希尔伯特式推演系统. 最常研究的希尔伯特风格演绎系统只有一个推理规则, 即肯定前件(MP)和几个无限公理模式:

Hilbert 的这套系统好处是很简单. 坏处是太难用了.

自然演绎系统(Gerhard Gentzen 提出)做了相反的取舍, 包括了很多演绎规则但有非常少甚至没有公理模式. 它(例如Finch-style, Jaśkowski style)基于一套引入(introduction)和消去(elimination)的规则⁴.

那我们教科书上的这套演绎规则是什么呢?

规则 P(引入前提): 可引入前提集合中任意一个前提.
规则 T(引入结论): 可引入逻辑蕴含式 + 基本等价公式作为已知结论.

命题公式的等价公式上面我们已经给出了, 这里是另外一些基本的逻辑蕴含式:

以上公式可以打表证明.

利用 \(P, T\) 规则的证明称为直接证明.

规则 CP(附加前提): 如果 \(\Gamma\wedge P\Rightarrow S\), 那么 \(\Gamma\Rightarrow P\rightarrow S\).
正确性: \(P\rightarrow(Q\to R)\Leftrightarrow(P\land Q)\rightarrow R\).

使用附加前提的证明称为条件证明. 我们再给出一种特殊的条件证明: 反证法

我们将结论 \(R\) 的否定 \(\neg R\) 作为附加前提作为条件, 倘若得到了 \(\Gamma \wedge \neg R\) 为矛盾式, 那么 \(R\) 为真.

事实上还可以证明命题逻辑的可靠性(soundness), 即: 凡是系统中可证明的都是系统的语言的重言式. 同理我们有完全性(completeness), 任何重言式都可以在系统中被证明.

谓词逻辑

我在学语法吗?

谓词逻辑, in short, 就是把命题逻辑中的原子命题进一步分解. 我们举个例子:

地球绕着太阳转.

可以分解成: 地球-绕-太阳, 那么我们用 绕(x, y) 表示 x 绕着 y, 它的值域是 0 和 1. 这里 绕(..) 就是所谓"谓词".

换言之, 谓词(predicate): 返回 bool 的一个函数.

既然也是 true or false, 问题来了: 谓词是一个命题吗? 这个问题等价于 x == 1 是命题吗? 显然不是. 因为 x 不确定.

谓词要成为命题, 需要赋值. 例如 绕(地球, 太阳) 就是一个命题. 实际上, 我们一般研究的是一阶谓词逻辑, 也就是变量数为一的情形. 一般来说, 我们会这么符号化: 绕(x) 为 x 绕着太阳转.

你可能会好奇: 不是说好了主谓宾吗? 怎么谓词还包含宾语呢? 实际上, 绕(x) = 绕(x, c), 而 c = 太阳, 因为我们把太阳看成了常量, 因此这个可以降为一阶谓词.

当然, 一般我们都会用符号来表示这些文字, 因此 \(P(x)\) 就是我们研究谓词的一般形式.

更严格来说, \(x\) 也称为个体词, 或者说项. 它可以是常量 \(1,2,...\), 也可以是变量 \(x, y,...\), 也可以是函数 \(x^2,\cos y,...\). 所谓谓词就是一个 \(D^{n} \to \{0,1\}\) 的一个映射.

命题需要范围: 量词

之前提过, 如果谓词想要成为命题, 就需要赋值. 例如: \(P(x): x \text{ is prime}\), 我们给定 \(x\) 的范围是 \(0 \leqslant x \leqslant 5\), 那么命题

\[P(0) \wedge P(1) \wedge P(2) \wedge P(3) \wedge P(4) \wedge P(5)\]

就表示 \(P(x)\) 在 \(0 \leqslant x \leqslant 5\) 上是否都满足条件.

\[P(0) \vee P(1) \vee P(2) \vee P(3) \vee P(4) \vee P(5)\]

就表示 \(P(x)\) 在 \(0 \leqslant x \leqslant 5\) 上是否有一个满足条件的项.

因为这么写太麻烦了. 而且对于某些无穷集, 如 \(\mathbb{N}^{+}\), 显然枚举到头也不是个办法, 因此我们引入了量词.

全称量词 \(\forall\) 就是用来表示"所有, 全部".
存在量词 \(\exists\) 就是用来表示"存在, 至少".

上面的例子就可以改写为

\(\forall x, P(x), x\in \{x|0\leqslant x \leqslant 5\}\)
\(\exists x, P(x), x\in \{x|0\leqslant x \leqslant 5\}\)

注意到 \(x\) 的个体域描述的也是关于 \(x\) 的一个性质, 那么我们也可以用一个特性谓词来描述 \(x\) 的个体域, \(x\) 现在就代表一个宽泛的全总个体域. 例如 \(H(x): 0 \leqslant x \leqslant 5\), 那么上面的例子又可以改写为

\((\forall x)(H(x)\to P(x))\)
\((\exists x)(H(x)\land P(x))\)

注意全程量词和存在量词在添加特性谓词的方式是不同的. 全称量词是析取, 存在量词是合取.

Remark 1: 注意量词否定需要转换.

Remark 2: 析取没有全称量词下的分配律, 合取没有存在量词下的分配律. 这很好理解, 因为所指不是同一个变量, 量词的辖域(影响的 \(x\) 的范围)很重要:

\[(\exists x)H(x)\land (\exists x)P(x)=(\exists x)H(x) \land (\exists y)P(y)\]

\[(\forall x)H(x)\to P(x)=\neg (\forall x)H(x)\vee P(x)=(\exists x)(\neg H(x) \vee P(y))\]

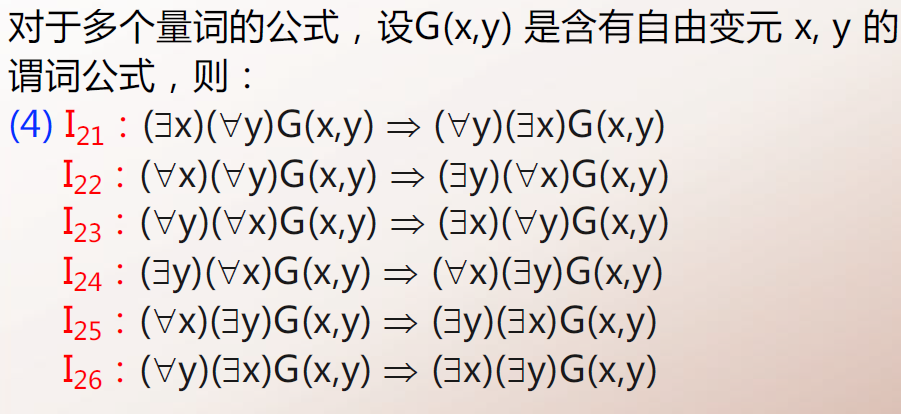
前束范式

前束范式是对含量词的范式的规范. 它的形式是: 所有谓词都处于公式的开头且不包含否定词, 它们的作用域延伸到整个公式的末尾.

\[ (\square x_1)(\square x_2)...(\square x_n) M(x_1,x_2,...,x_n) \]

定理任意一个谓词公式均可化为与之等价的前束范式.

求前束范式的关键就是要记住量词辖域收缩与扩张等值式.

量化命题的推理规则

US(Universal Specify):
- \((\forall x )G(x)\Rightarrow G(y)\) (\(y\) 为任意的个体变量, 不在 \(x\) 中出现)
- \((\forall x )G(x)\Rightarrow G(c)\) (\(c\) 为任意的个体常量)
UG(Universal Generalize): \(G(y)\Rightarrow (\forall x)G(x)\)
ES(Existential Specify): \((\exists x)G(x)\Rightarrow G(c)\) (\(c\) 特定的个体常量)
EG(Existential Generalize):
- \(G(c)\Rightarrow (\exists x)G(x)\): \(c\) 为特定的个体常量, \(G(c)\) 中无自由变元 \(x\)
- \(G(y)\Rightarrow (\exists x)G(x)\): \(G(y)\) 不含自由变元 \(x\)

四条规则仅对前束范式适用.

参考资料

离散数学及应用原书第五版, Kenneth H. Rosen, 机械工业出版社
离散数学及其应用(第三版), 傅彦等, 高等教育出版社
符号逻辑讲义, 徐明(图书馆五楼有!)
Farmer, W. M. Propositional logic
校内 PPT

也称善意推定.↩︎
也叫做合式公式, 问题是有什么公式是不合式的?↩︎
是上文提到的文字(literal).↩︎
感兴趣可以参考 Logic in Computer Science 一书.↩︎