简单的数据结构

发表于 更新于 分类于 本文字数： 5k 阅读时长 ≈ 18 分钟

做一个数据结构的小小总结. 其实数据结构和算法是不分家的, 例如 1+1=2 是一个加法算法, 用到了整型的数据结构 1. 你就说是不是吧.

DSA课程/书本上更注重实现. 手搓一个泛型结构, 实现 std 里头的一堆方法, 这不劝退谁劝退. 实现是为了更好理解原理. 不要被复杂的构造带偏了学习的方向! 我们实现的标准是: ANSI C 也能做到!

剩下的内容: 怎么用STL来解决使用到特定数据结构的题目, i.e. 会做题. 但我们也懂原理!

链表

静态链表

我们用数组模拟链表. 动态链表谁不会啊?

1
2
3
4
5
6
struct Node
{
    int val;
    Node *next;
};
new Node(); // TOO SLOW! 除非你用内存池优化

数组模拟单链表: 效率高 最大用处是邻接表 邻接表能拿来储存图/树.

储存方式: 区别于动态链表, 每个值对应一个地址, 静态链表采用编号的形式.

略过头节点, 第一个节点编号为 0, 然后是 1, 直到下一个节点不存在, 这个next节点编号为-1. 编号和下标关联起来, 通过访问编号, 也就访问了相应的元素值.

1
int head, e[N], ne[N], idx;

把 x 插到链表第 k 个元素之后, 要考虑插入的位置. 如果 k = 0, 那么就把新节点设置为头节点即可:

1
2
3
newNode->data = data;
newNode->next = head;
head = newNode;
1
2
3
4
5
6
7
8
9
// 找到第 k 个节点
Node* current = head;
for (int i = 1; i < k && current != NULL; i++) {
    current = current->next;
}
// 然后插入新节点
newNode->data = data;
newNode->next = current->next;
current->next = newNode;

作为对比, 我们来关注下静态链表的实现:

1
2
3
4
// 头节点插入 x
e[idx] = x;
ne[idx] = head;
head = idx++;
1
2
3
4
// x 插入到下标为 k 的后面
e[idx] = x;
ne[idx] = ne[k];
ne[k] = idx++;

静态链表表示的含义基本上和动态链表无异. 唯一的区别就是最后要手动更新下标idx. 此外, 这种规定下, 第一个节点的下标为0, 实际操作可能要对下标偏移一位. 例如 insert(k - 1, x) 表示在第 k 个节点后插入 x. 当然你也可以将 idx 初始化为 1. 你会发现静态链表实际上有空间换时间的做法. 因为多了一个 ne 数组, 我们访问下标要比动态链表遍历找到第 k 个元素快的多.

删除操作, 实际上就是当原节点不存在, 并没有真正地在内存上把它抹除:

1
ne[k] = ne[ne[k]];

双链表

双链表多了一个 prev(前驱指针), 操作其实和单链表没多大区别.

我们规定 head: 0 (头节点) tail: 1 (尾节点) 这两个节点不储存值, 表示链表的头尾 怎么初始化? ne[0] = 1, prev[1] = 0, idx 0 和 1 表示头和尾 然后 idx 就从 2 开始.

双链表新增的操作是往左边插入, 实际上就是 add(prev[k + 1], x).

链表就像看图说话. 看着图就知道代码怎么写了.

双链表能优化某些问题.

栈

先进后出

数组模拟: stk[N], tt

push(x) 就是 stk[++tt] = x (栈指针+1, 然后赋值) pop(x) 就是 tt-- (栈指针-1) query() 返回栈顶元素 stk[tt]

很自然的实现方式. 理解以后就不难理解汇编的函数栈.

应用: 表达式求值

模拟样例: 计算 2*(5-3), 2, *, (, 5, -, 3 依次入栈, 当读到 ) 时开始出栈, 直到 ( 停下, 也即 3, -, 5, ( 出栈并计算, 结果为 2, 入栈, 然后出栈 2, *, 2 并计算, 入栈 4, 然后打印栈顶元素.

单调栈

要求: 输出每个数左边第一个比它小的数

暴力做法:

1
2
3
4
5
6
7
for (int i = 0; i < n; i++)
    for (int j = i - 1; j >= 0; j--)
        if (a[i] > a[j])
        {
            cout << a[j] << endl;
            break;
        }

优化: 所有逆序元素可以删掉 最后维护一个单调的栈 考虑 3 2 4 7 5 6, 对于 4 而言 2 是它的目标值, 而 3 之后再也不会用到了, 因为 2 比它更靠后, 且比它更小. 于是 3 可以删去, 并且不影响问题. 对于 5 而言, 4 是它的目标值, 中间多插入了一个 7, 是逆序的, 因此 7(栈顶元素) 可以删去.

要判断的是 stk[tt] < a[i].

1
2
3
4
5
6
7
8
9
10
11
12
13
for (int i = 0; i < n; i++)
{
    int x;
    cin >> x;
    while (tt && stk[tt] >= x)
        tt--;
    if (tt)
        cout << stk[tt] << ' ';
    else
        cout << -1 << endl;

    stk[++tt] = x;
}

例题: Codeforces Edu. Round 156(Rated for Div 2): C. Decreasing String

队列

先进先出

模拟队列和模拟栈是类似的, 多了一个队尾

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int hh = 0, tt = -1;
void push(int x) {
    q[++tt] = x;
}
void pop() {
    hh++
}
bool empty() {
    if (tt >= hh) return false;
    else return true;
}
// 返回队头元素
int front() {
    return q[hh];
}

单调队列

比喻: 公司来了一个更年轻的新人, 如果他比一些老员工还要优秀, 那么这些老员工就会被立即淘汰(从队列中删除), 如果没有老员工优秀, 那么老员工会一直干到退休然后被淘汰(从滑动窗口中出去)

模板题: 长度为 \(n\) 的序列当中, 求每个长度为 \(m\) 的区间区间最值. 时间复杂度为 \(O(n)\).

单调队列

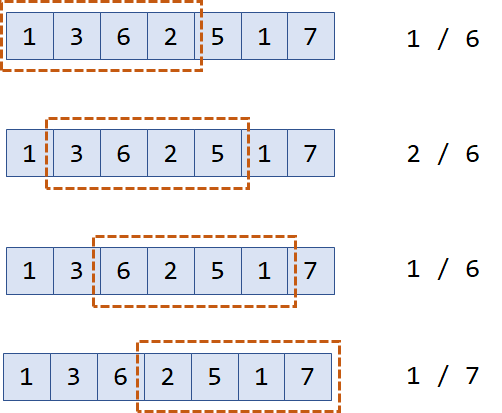
假设我们求的是区间最大值. 实际上每个滑动窗口中的队列为: 6,2 -> 6,5 -> 6,5,1 -> 7

队列中成员单调递减(或递增), 因此称这个队列为单调队列.

滑动窗口问题:

  • 普通队列怎么做
  • 将队列中没有用的元素删掉(单调性)
  • 取队头/队尾 O(1)

本质上这是一个双端队列(deque). 用数组模拟可以这么实现(在队列的基础上拓展):

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int hh = 0, tt = -1; // 队列存储下标
for (int i = 0; i < n; i++)
{
    // i 是窗口的右端点 i-k+1 右端点
    // 如果队头元素在窗口内部
    // 那么就将队头元素后移
    if (hh <= tt && q[hh] < i - k + 1)
        hh++;
    // 保证队尾元素大于等于右端点的值
    while (hh <= tt && a[q[tt]] >= a[i])
        tt--;
    // 将 i 入队
    q[++tt] = i;
    if (i >= k - 1)
        cout << a[q[hh]] << ' ';
}

用 STL 可以这么写(更符合抽象思维):

1
2
3
4
5
6
7
8
9
10
11
12
deque<int> q; // 存储的是编号
for (int i = 0; i < n; i++)
{
    if (!q.empty() && i - q.front() >= k)
        q.pop_front();
    while (!q.empty() && v[q.back()] >= v[i])
        q.pop_back();

    q.push_back(i);
    if (i >= k - 1)
        cout << v[q.front()] << ' ';
}

求最大值可以对称过去. 很容易处理.

单调队列可以优化部分dp问题.

字符串

KMP

见其它文章.

Trie树(字典树)

高效存储字符串及查找.

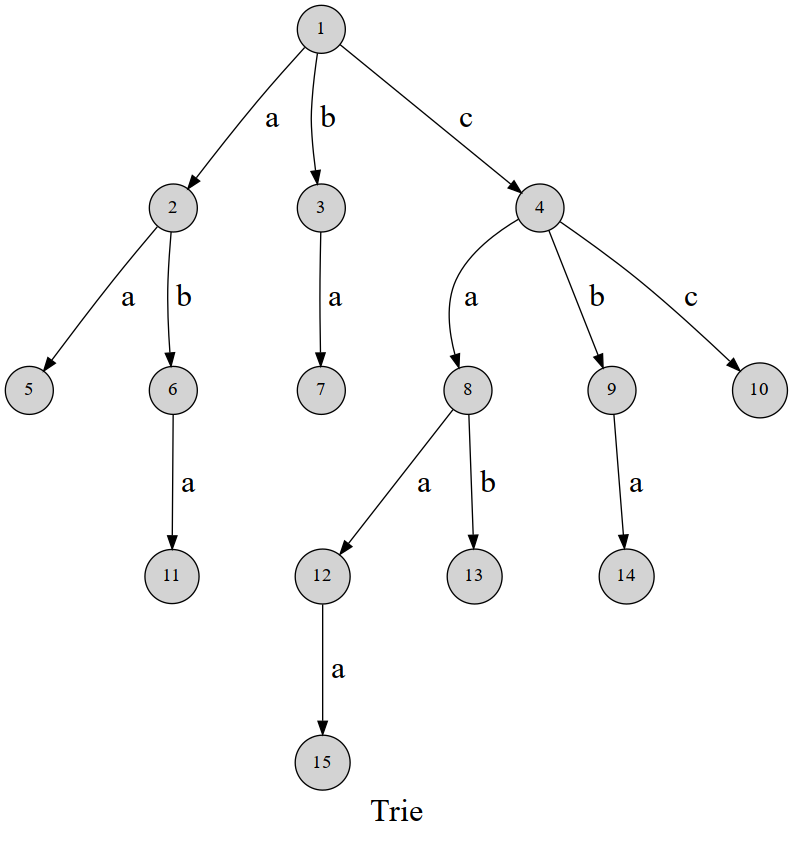
Trie1

每个节点存放它的编号.

1
2
3
4
5
6
7
8
9
10
11
12
13
int son[N][26], cnt[N], idx;
void insert(string str)
{
    int p = 0;
    for (int i = 0; str[i] != '\0'; i++)
    {
        int u = str[i] - 'a';
        if (!son[p][u])
            son[p][u] = ++idx;
        p = son[p][u];
    }
    cnt[p]++;
}

应用: 最大异或值

用字典树存储一个树的二进制表示

1
2
3
4
5
6
7
8
9
10
11
void insert(int x)
{
    int p = 0;
    for (int i = 30; ~i; i--)
    {
        int &s = son[p][x >> i & 1];
        if (!s)
            s = ++idx;
        p = s;
    }
}

并查集

作用/功能:

  1. 将两个集合合并 近乎O(1) 2
  2. 询问两个元素是否在同一个集合当中

基本原理: 每个集合用一棵树来表示, 树根的编号就是整个集合的编号. 每一个节点存储它的父节点, p[x] 表示 x 的父节点.

并查集

初始化: 每个数位于单独的集合. 每个数的父节点都是它自己. std::iota(p.begin(), p.end(), 0)

问题1: 如何判断树根 if(p[x] == x)

问题2: 如何求 x 的集合编号 while(p[x] != x) x = p[x]; 这个可以写成递归的形式

问题3: 如何合并这两个集合 p[x] = y 让加入集合的根节点作为原集合根节点的儿子

*启发式合并: 选择哪棵树的根节点作为新树的根节点会影响未来操作的复杂度, 可以将节点较少或深度较小的树连到另一棵 当然这个是optional, 通常不采用启发式合并题目也能过的.

优化: 路径压缩 按秩合并(不考虑)

保证树是双层的.

具体实现: find(x) 返回 x 的祖宗节点 如果是根节点就返回自己 递归实现 p[find(x)] = find(y) 实现合并操作. 注意对根节点进行 find 操作就等同于返回它自身.

难点:

  • 理解 find 函数里的递归
  • 合并时的 p[find(i)] = find(j)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n, m;
int p[N];
int find(int x)
{
    if(p[x] != x)
        p[x] = find(p[x]);
    return p[x];
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
        p[i] = i;
    while (m--)
    {
        char op[2];
        int a, b;
        cin >> op >> a >> b;
        if(op[0] == 'M')
            p[find(a)] = find(b);
        else
        {
            if(find(a) == find(b))
                cout << "Yes" << endl;
            else
                cout << "No" << endl;
        }
    }
    return 0;
}

经典题目: POJ1182 食物链

有生之年能做完的习题集 并查集

图

一些图论基础:

图 = 顶点+边 的集合

用 \(G(V,E)\) 表示. G: Graph V: Vertex E: Edge

边的方向: 有向图和无向图 带权和不带权: 边可以有权重, 可以表示诸如距离或者时间之类的量

图的存储

  • 直接存边 例如 Kruskal 算法
  • 邻接矩阵 很符合直觉的一种方式
  • 邻接表 链表升级版

可以用一个二维数组表示一个图, 这个数组又被称为邻接矩阵.

a[i][j] 表示顶点 i 到 j 是否连通. 如果连通, 那么这个值为 1, 否则为 0. 在带权图中, 这个值为 i 到 j 所需要的边权值(如距离, 时间etc.) +inf 表示不连通(无法到达).

对于无向图, 邻接矩阵关于主对角线对称. 对角线为 0, 表示某定点到自己的边长为 0(对于简单图而言).

邻接矩阵的优点: O(1) 的查询时间

我们也可以用链表来表示一个图, 这种方法也被称为图的邻接表.

  • 存放有关边的信息, 只存邻居点的信息
  • e[u][i] 表示节点 u 的第 i 条边

我们一般使用邻接表来表示稀疏图, 邻接矩阵表示稠密图.

如果要存储带权的边, 在定义节点结构的时候可以附带存储一个变量.

链式前向星

  • 用静态数组模拟邻接表的方式
  • 比较复杂, 建议结合图片食用

习题: 树的重心

核心思想: DFS 枚举图中的每一个点, 求出"向下"子树的最大大小, 然后利用总结点数 - 子树大小之和, 得出"向上"子树的大小, 每次 DFS 依照定义更新 min(ans, max(res, n - sum)).

P1364 医院设置: 带权的树的重心

二叉树

注: 本题的综合性比较高.

导航: 1497. 树的遍历

这道题很classic. 怎么花式去遍历一棵树: 后序遍历 中序遍历 层序遍历

解释下什么意思:

1
2
3
4
5
     1
   /   \
  2     3
 / \   / \
4   5 6   7
  1. 后序遍历: 4 -> 5 -> 2 -> 6 -> 7 -> 3 -> 1
  2. 中序遍历: 4 -> 2 -> 5 -> 1 -> 6 -> 3 -> 7
  3. 层序遍历: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7

输入后序遍历和中序遍历, 可以确定一棵二叉树.

通过后序遍历找到根的值, 然后再到中序序列里找到根的位置再将该树分为左子树与右子树(对应区间分割), 然后不断递归即可通过中序和后序重塑一棵树.

例如找到了后序遍历到了2, 那么在中序遍历中找到这个2, 2前后的两个元素, 即 4 和 5, 也就是一个 parent 2 和 left child 4 和 right child 5. parent 可以看成是一个树的 root.

一个难点是怎么确定 left child 和 right child 在后序遍历中的位置. 解决方案如下: 因为我们知道中序遍历的区间范围, 也即知道了左树和右树的大小, 而利用这个大小不会变我们可以反推: pr' = pl + (k - 1 - il)(左树的情形), pl' = pl + (k + 1 - il) - 1(右树)

问题: 为什么要-1? 答案: 因为index从零开始取的

因为存在在中序遍历搜索后序遍历里的值的过程, 因此中序遍历用一个hash表存放.

代码很精巧. 建议反复阅读orz

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <bits/stdc++.h>
using namespace std;

const int N = 40;
int n;

int postorder[N], inorder[N];
unordered_map<int, int> l, r, pos;

int build(int il, int ir, int pl, int pr)
{
    int root = postorder[pr];
    int k = pos[root];
    if (il < k)
        l[root] = build(il, k - 1, pl, pl + k - 1 - il);
    if (ir > k)
        r[root] = build(k + 1, ir, pl + k - il, pr - 1);
    return root;
}

void bfs(int root)
{
    queue<int> q;
    q.push(root);
    while (q.size())
    {
        auto t = q.front();
        q.pop();
        cout << t << ' ';
        if (l.count(t))
            q.push(l[t]);
        if (r.count(t))
            q.push(r[t]);
    }
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n;
    for (int i = 0; i < n; i++)
        cin >> postorder[i];
    for (int i = 0; i < n; i++)
    {
        cin >> inorder[i];
        pos[inorder[i]] = i;
    }
    int root = build(0, n - 1, 0, n - 1);
    bfs(root);
    return 0;
}

线段树

树状数组

树状数组 Binary Index Tree, BIT, Fenwick Tree

应用场景

  • 单点修改: 更改数组中一个元素的值
  • 区间查询: 一个区间内所有元素的和

时间复杂度均为 \(O(\log n)\)

感受: 求 a[1...n] 的前缀和

\(O(n)\) 扫描一遍

1
2
for (int i = 1; i <= n; i++)
    s[i] = s[i - 1] + a[i];

但是一旦某一个元素更改, 又得重新更新一遍 s 数组

问题: 如果我们能够把 [1,n] 拆成不多于 \(\log n\) 段区间...

线段树

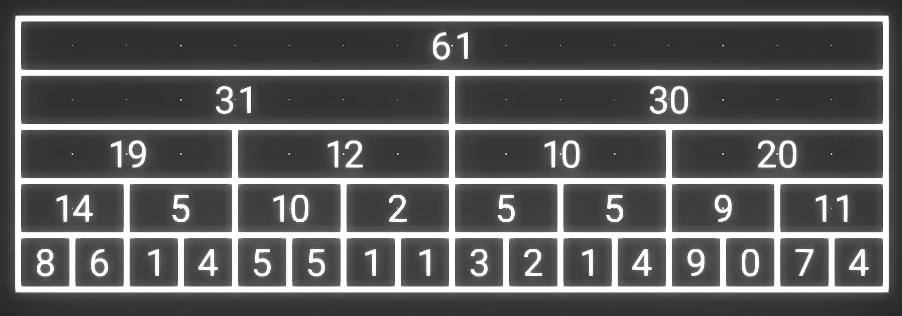
用线段树表示

这样表示前 5 个元素的和, 你就可以用 a[1..4]+a[5]

观察: 总有更优的结构

  • 例如有 a[1..4] 就不需要 a[3..4], 只需要保留 a[1..2]
  • 进一步...
    • a[2] 也不需要了, 因为 a[2] = a[1..2]-a[1], 用 a[1..2] 取代 a[2]
  • 所有层的第偶数个数字都是没有必要的

删去冗余数字后, 剩下数字的数量恰好有 n 个. 剩下的这个数组就是我们要的树状数组

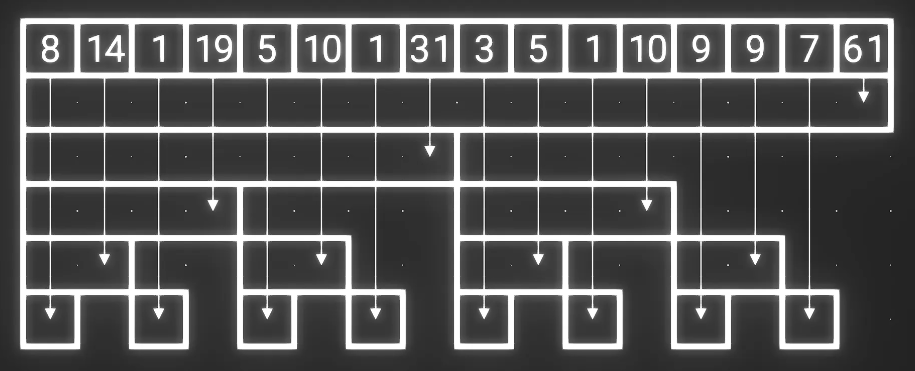
fenwick tree

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
template <typename T>
struct Fenwick
{
    int n;
    std::vector<T> a;

    Fenwick(int n = 0) { init(n); }

    void init(int n)
    {
        this->n = n;
        a.assign(n, T());
    }

    void add(int x, T v)
    {
        for (int i = x + 1; i <= n; i += i & -i)
            a[i - 1] += v;
    }

    T sum(int x)
    {
        auto ans = T();
        for (int i = x; i > 0; i -= i & -i)
            ans += a[i - 1];
        return ans;
    }

    T rangeSum(int l, int r) { return sum(r) - sum(l); }

    int kth(T k)
    {
        int x = 0;
        for (int i = 1 << std::__lg(n); i; i /= 2) {
            if (x + i <= n && k >= a[x + i - 1]) {
                x += i;
                k -= a[x - 1];
            }
        }
        return x;
    }
};

桶

应用:

  • 桶排序
  • 计数器数组

例如计算字符串中两个相同字符之间的距离, 可以这么写

1
2
3
4
5
6
7
8
9
int cnt[N];
memset(cnt, -1, sizeof cnt);
for (int i = 0; i <= n; i++)
{
    if(cnt[s[i]] != -1)
        cout << s[i] - i << endl;
    else
        cnt[s[i]] = i;
}

哈希表(散列表)

哈希表

key-value 式的数据结构, 有 key 就能查询到 value, 实际上是一种映射. 这个 key 可以是 int, string, 甚至结构体. 可以把哈希表理解成一种高级的数组, 下标就是 key, key 对应值在内存的位置.

通过一个哈希函数 h(x) 假设我们用数组 a 存放数据, 那么 (key, value) 就应该放在 a[h(key)] 上.

一个应用: 数据量 N 0~1e9 中的数字映射到 0~1e5 哈希函数怎么取? h(x) = x mod M M 是一个大质数

Remark: 离散化是一种及其特殊的哈希(离散化是保序的)

  • \(x \bmod 10^5\)
  • 哈希冲突怎么办? (两个不同数据, 但哈希值相同)
  • 抽屉原理告诉我们这是不可避的.
    • 拉链法/开散列表(open hashing): 储存当前槽上存储的数(类似邻接表)
      • 查询的时候扫描链表就行.
    • 开放寻址法/闭散列法: 如果插入数据的位置上已经有数据, 就插入到下一个空余位置(比喻: 上厕所)
      • 有线性探测, 二次探测, 双重散列(双哈希)等方法...
      • OI 里一般用的是拉链法.

实现操作: 比赛里(一般)只会有添加和查找两个操作

MD5, SHA-1 背后原理都是 hash.

std 库的哈希表

unordered_map 或者 unordered_set

1
2
3
4
5
6
unordered_map<int,int> mp;
// 添加操作
mp[x]++;
// 查询操作
if(mp[t] > 0)
    // code
1
2
3
4
5
6
unordered_set<int> hashmap;
// 插入操作
hashmap.insert(x);
// 查询操作
if(hashmap.count(t))
    // code

字符串哈希

比较重要的哈希方式 一些字符串问题不一定需要KMP 字符串前缀哈希法 h[i] 表示前缀字符串对应的哈希值

问题: 如何定义某一前缀字符串的哈希值?

我们采用多项式 Hash 的方法.

字符串P进制下的 "ABCD"-> A B C D -> 1 2 3 4 -> 十进制数 \(1\cdot p^3 + 2 \cdot p^2 + 3 \cdot p^1 + 4 \cdot p^0\) 最后对整个数取模 \(q\) 字符串就映射到了 0~q-1

公式化: 对于一个长度 \(l\) 的字符串 \(s\), 那么它对应的哈希函数值为

\[f(s) = \sum^{l}_{i=1}s[i]p^{l-i}\]

不能映射成 0 (A 0 那么 AA 也是 0) 字符串的哈希方法不考虑冲突的情况 经验值 p = 131 或 p = 13331 q = 2^64 在一般情况假定不会出现冲突(冲突概率约为 \(|s|-1/q\))

用 unsigned long long 可以省去 mod 2^64(因为溢出就等同于取模, 见CSAPP Chapter 2)

类似前缀和, 如果想求 L 到 R 这一段的hash, 那么可以按照下面的方式

\[h_R - h_{L-1} \cdot p^{R-L+1}\]

你可以手动代入计算这个是否正确.

应用: 字符串匹配.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;

const int N = 1e5 + 5, P = 131;
int n, m;
char str[N];
ULL h[N], p[N];

ULL get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> m >> (str + 1);
    p[0] = 1;
    for (int i = 1; i <= n; i++)
    {
        p[i] = p[i - 1] * P;
        h[i] = h[i - 1] * P + str[i];
    }
    while (m--)
    {
        int l1, r1, l2, r2;
        cin >> l1 >> r1 >> l2 >> r2;
        if (get(l1, r1) == get(l2, r2))
            cout << "Yes" << endl;
        else
            cout << "No" << endl;
    }
    return 0;
}

堆

堆实现

STL里的数据结构为 priority_queue 优先队列实现堆 基本功能:

  • 插入一个数
  • 求集合中的最小值
  • 删除最小值
  • 删除任意一个元素(STL无)
  • 修改任意一个元素(STL无)

堆是一棵完全二叉树.

小根堆: 每个点都小于它的左右child, 那么根节点就是最小值

堆的存储: 一维数组, 下标从1开始.(因为0的左child也是0, 不方便) 下标 x 的左child: 下标 2x 右child: 2x+1

down(x): 让一个节点往下移动 up(x): 往上移动

所有操作可以用这两个基本操作实现:

插入: 原堆大小为 size 那么 heap[++size] = x; up(size) 即可. 最小值: heap[1] 删除第一个元素: 用堆里最后一个元素覆盖掉第一个元素heap[1] = heap[size], 然后size--, 维护根节点 down(1) 删除任意元素: heap[k] = heap[size], size--, down(k), up(k)(只会执行一步up/down操作). 修改任意元素: heap[k] = x, down[k], up[k]

利用二叉堆实现堆排序. 只用实现down:

1
2
3
4
5
6
7
8
9
10
11
12
13
void down(int k)
{
    int t = k;
    if (k * 2 <= s && heap[k * 2] < heap[t])
        t = k * 2;
    if (k * 2 + 1 <= s && heap[k * 2 + 1] < heap[t])
        t = k * 2 + 1;
    if (k != t)
    {
        swap(heap[k], heap[t]);
        down(t);
    }
}

然后不断向堆插入元素即可.

std 库里的堆

用优先队列 priority_queue<T, vector<T>, ...>

最后一个可以填 greater<T>, 表示小根堆; less<T> 表示大根堆.

  1. 严格来说这不算是一个"结构", 而是简单的类型. 只要你懂我意思就行 :)↩︎

  2. 关于时间复杂度的证明, 可以看这篇文章.↩︎