保研, 相亲, 找工作——背后的稳定匹配问题
稳定匹配问题(Stable Matching Problem)最早出自 D.Gale 和 L.S.Sharpley 1962年发表在美国数学月刊上的一篇关于大学录取和婚姻稳定的文章1. 解决这个问题的算法出奇地简单, 甚至是自我执行(self-forcing)的——换言之, 不需要系统的调度, 就能获得令人满意的结果!
本文重点陈述算法的正确性——作为离散数学中逻辑命题与证明的简单应用.
问题描述
问题描述: 考虑你经营一家雇佣系统, 任务将 \(n\) 个职位和 \(n\) 名候选人匹配起来. 每项工作对 \(n\) 名候选人有一排序的倾向表, 每位候选人也有类似的表.
例如, 考虑 \(n=3\), 为简化, 我们假设候选人为 A, B, C, 岗位为 1, 2, 3. 对于 A, 他的倾向表为 2, 1, 3, 表示最希望分配到2, 1次之, 3最后. 同样的, 岗位1选人的倾向表为 A, C, B, 表示最希望招到 A, C次之, B最后.
我们的目标是: 最大化总满足度, 最大化每个人的第一选择, 以及减少倾向排名的差距
Gale-Shapley 算法 (a.k.a. The Propose-and-Reject Algorithm)
对于每一天:
- 每个职位向它列表上最希望的候选人发offer.
- 每个候选人都可以拒绝非自己最期望的offer. 已得的offer会置于一个string上.
- 被拒绝的职位会在表上划去拒绝人的名字.
当每个人都拿到offer的时候, 程序停止.
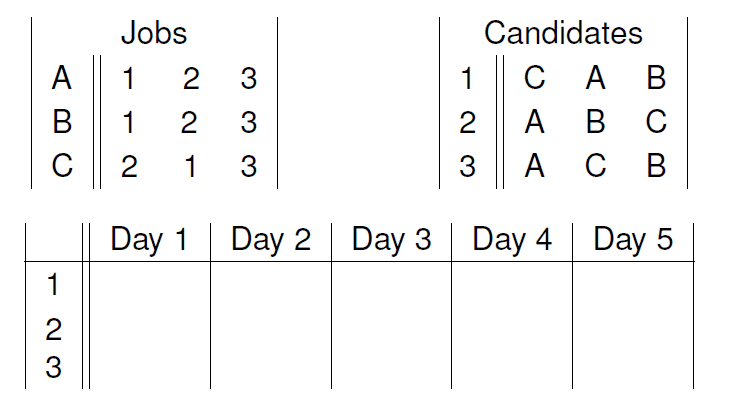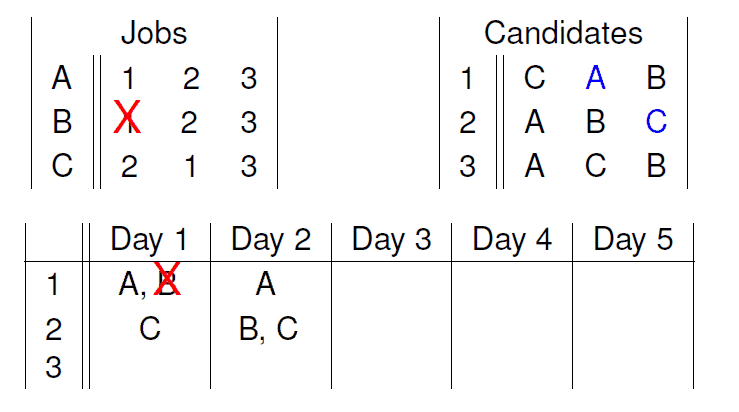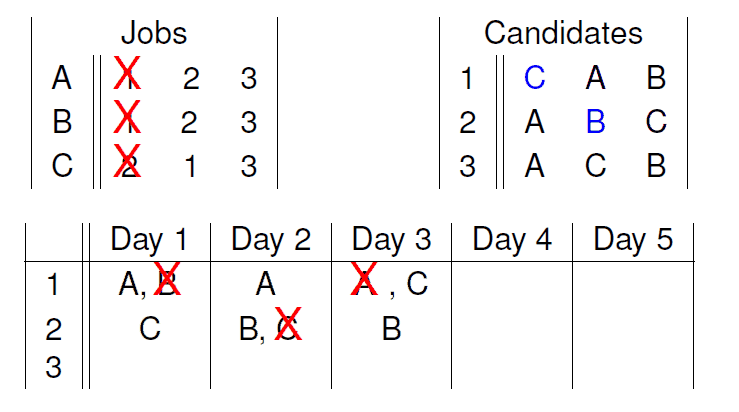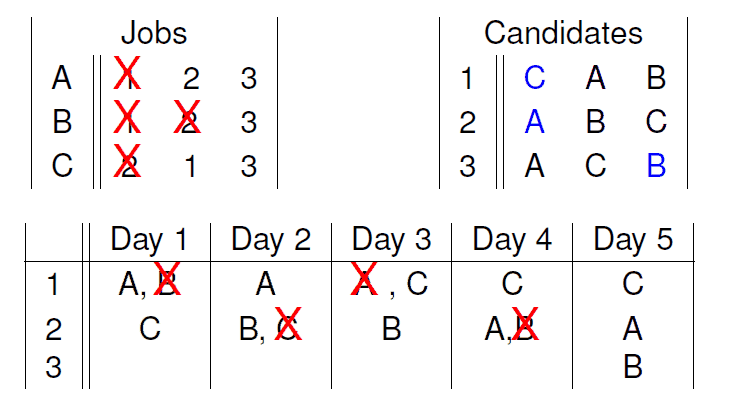
Before: 符号定义
定义 1 包含 \(n\) 对 pair 的不交集, 称为匹配 \(S\).
例如: \(S = \{(1, A), (2, B), (3, C)\}\) 就是一个包含 \(3\) 对 pair 的匹配.
定义 2 如果 \(b\) 比起 \(g\) 更喜欢 \(g^{*}\), 记 \(g^{*} > g\). 特别地, 如果 \(b\) 认为 \(g^{*}\) 至少和 \(g\) 一样好, 记 \(g^{*} \geqslant g\), 当且仅当 \(g^{*} = g\) 取等.
定义 3 对于匹配 \(S\) 中的元素 \(b, g^{*}\): 如果 \(b, g^{*}\) 是比当前 partner 更优的一对, 则称 \(b, g^{*}\) 为一对rouge couple.
例如: 假设对 \(1\) 有 \(C>B\), \(C\) 认为 \(1>2\), 那么匹配 \(S = \{(1, B), (2, C)\}\) 中存在 rouge couple \(1, C\).
定义 4 不存在 rouge couple 的匹配 \(S\) 称为稳定匹配. 否则则为不稳定匹配.
在上面的例子中: 因为 \(1\) 可以追求 \(C\), 同时 \(C\) 也会欣然接受 \(1\), \((1,B)\) 及 \((2,C)\) 都有决裂的可能, 因此 \(S\) 是一个不稳定匹配.
证明
总能停下
引理 1 算法总能停下.
证明 算法尚未停止时, 每一天结束至少有一家公司将应聘者的人名从列表上划去. 因为列表有 \(n\) 份, 每份上有 \(n\) 个元素, 因此算法至多在 \(n^2\) 的迭代(天)下终止.
进步引理
引理 2 对于第 \(t\) 天, 候选人 \(g\) 手上有职位 \(b\), 那么第 \(t'\) 天结束, 他手上的 \(\forall b'\) 至少和 \(b\) 一样好, 其中 \(t' > t\).
证明 我们对天数 \(i\geqslant k\) 归纳.
当 \(i = k\), \(C\) 可以收到至少一份offer(来自 \(J\)). 在第 \(k\) 天结束, \(C\) 手上至少会有 \(J\) 或者比 \(J\) 更好的offer(他可以自行选择).
对于 \(\forall i \geqslant k\) 的情况, 假设命题成立, 只需归纳证明对 \(i+1\) 命题同样成立.
根据我们的假设, 第 \(i\) 天 \(C\) 获得了 \(J'\geqslant J\), 根据算法, \(J'\) 在第 \(i+1\) 天依然会向 \(C\) 给出offer(因为 \(C\) 在第 \(i\) 天没理由拒绝或者 \(J'\) 凭空消失). 因此当第 \(i+1\) 天结束, \(C\) 手上要么是 \(J'\), 要么是比 \(J'\) 更好的offer; 两种情况都 \(\geqslant J\), 因此结论对第 \(i+1\) 天成立.
正确性
引理 3 Gale-Sharpley算法得出的匹配不存在rouge couple.
证明 反证法. 假设存在 \((b,g^{*})\), 且当前匹配为 \((b,g),(b^{*},g^{*})\). \(b\) 比起 \(g\) 更喜欢 \(g*\), 在给 \(g\) 发出offer之前先给 \(g^{*}\) 发出了offer, 而 \(g^{*}\) 拒绝了 \(b\), 由引理 2, 知 \(g^{*}\) 比起 \(b^{*}\) 更喜欢 \(b\), 与条件矛盾.
定理 1 Gale-Sharpley 算法是一种稳定的匹配算法.
证明 由引理 1 和引理 3 可知其正确.
最优性: 对谁更有利?
定义 5 如果 \(x\) 的 partner 在任何稳定匹配下皆为它的最佳 partner, 称匹配为 \(x\) 最优的.
同样可以给出 \(x\) 最劣的定义.
定义 6 如果对全部工作/候选人 \(x\) 都是 \(x\) 最优的, 称匹配为工作/候选人最优.
例子: A:1,2 B:2,1 1:A,B 2:A,B
S: (A,1) (B,2) T: (A,2) (B,1)
S, T 都是稳定的. 但 S 是对 A,B 最优, T 对 1,2 最优.
定理 2 Gale-Sharpley算法是工作最优匹配.
证明 假设匹配对工作不是最优的: 存在 \(b\) 得不到最优候选人 \(g\). 存在稳定匹配 \(S\) 存在 \((b,g)\) 匹配. 令 \(t\) 为 \(b\) 被 \(g\) 拒绝的第一天, 那么在第 \(t\) 日有 \(b^{*}\) 与 \(g\) 匹配, 也就意味着 \(g\) 比起 \(b\) 更喜欢 \(b^{*}\). \(b^{*}\) 至少也会将 \(g\) 作为它的最优候选人看待, 也就推出了" \(b^{*}\) 比起他在 \(S\) 中的 partner \(g^{*}\) 更喜欢 \(g\) "的结论, 而 \(b,g^{*}\) 是一对rogue couple, 也即 \(S\) 是不稳定的, 也就发生了矛盾.
后记
TODO List:
- Talk is cheap, show me the code!
- 哪天写一个示例程序
- 可读性很烂, 加上纯数更难理解了.
- 哪天重构下段落和语句
- 想把证明方法背后的数学原理介绍给各位
- 例如反证法在数理逻辑上为什么是正确的
- 现在还只停留在介绍的阶段.
- 推荐读物里有本书, 哪天有空去找找看, 提取一些有意思的内容
- 多些深度和应用
拓展阅读
[1]. UCB CS70 Note 4: Stable Matching Problem
[2]. D. Gale and L.S. Shapley, “College Admissions and the Stability of Marriage,” American Mathematical Monthly 69 (1962), pp. 9–14.
[3]. D. Gusfield and R.W. Irving, The Stable Marriage Problem: Structure and Algorithms, MIT Press, 1989.
Matching领域的开山文章, 算法分析的伟大成就之一, 顺带一提 Sharpley 也是2012年诺贝尔经济学奖的得主. 题外话: 在文章的最后, 作者提到希望借此文章改变大众对数学/数学家的认知: 我们真的不是只懂"一堆公式", 不说人话的家伙; 还希望数学老师也能启发启发学生 :)↩︎