2023寒假每日一题

发表于 更新于 分类于 本文字数： 4k 阅读时长 ≈ 14 分钟

收录一些寒假做的题目. 题目来源: 寒假每日一题2023 我才不是水题大师呢, 因为蒟蒻所以只能做这些入门题, 但实际上更水的题目已经被我筛掉了 (

孤独的照片

导航: USACO 2021 December Contest, Bronze Problem 1. Lonely Photo

题目等价于: 长度大于等于3, 且子串中两种字符中的一种, 数量小于等于1, 求这些子串的数目. 示例: GHGHG 输出 3, 其中 GHG, HGH, GHG 就是题目要求的.

暴力枚举会超时. 自己思考这个问题, 你会发现这道题实际上是个排列组合问题. 高考数学遇到求 GGGGHGGGG 符合题目条件的子串, 你会怎么做? 分类讨论, 然后利用乘法原理:

  • H 左边连续的 G 有 4 个, 右边连续的 G 有 4 个.
  • 两边可以任选连续个数的 G, 左边可以不选, 也可以选1个, 一直到4个G; 右边也是同样的道理.
    • 如果左右各选一个 G, 最小子串为 GHG, 剩下各边还有 3 个连续的 G, 可以不选, 或者选1个, 一直到3个, 依乘法原理有 4 * 4 = 16.
    • 如果 H 作为子串的右端点, 最短子串为 GGH, 剩下可以不选, 或者选1个或2个. 那么有 4 - 1 = 3 种情况.
    • 如果 H 作为子串的左端点, 本例中有 4 - 1 = 3 种情况.
  • 一共有 16 + 3 + 3 = 22 种情况.

推广: ans = l * r + l - 1 + r - 1, 其中 l 表示"孤独"字符左边连续的另一字符的数量, r 同理. 一个问题是, 对于"孤独"字符处于端点的情况, l - 1 必须大于等于2, 否则构成不了最短子串. 因此可以做一个小操作: max(l - 1, 0). 然后依次遍历整个数组.

通过数学做法, 计算每一个字符和左右满足的子串, 时间复杂度压到了O(1).

接下来是获取每一个字符对应的 l 和 r. 用 g 表示连续遇到的 G, h 表示连续遇到的 H.

  • 如果下一个字符不同, 假设当前字符为 G, 下一个字符为 H, 那么将 g 储存在 l[i] 或者 r[i], 然后 g 归零, 因为不再连续.
  • 如果下一个字符相同, 那么 g 或者 h 自增, 然后将 g(或者 h) 存储在 l 或者 r 中.

本题也需要注意卡 int.

上课睡觉

导航: USACO 2022 February Contest, Bronze, Problem 2 Sleep in Class

本地化导航: AcWing 4366. 上课睡觉

题目要求: 合并, 石子堆集合中的每堆石子的数量都相同

假设总数 sum 的石子堆可以被平分成 i 堆, 每堆石子的个数为 cnt, 且易知 cnt = sum / i.

因为每次合并操作会使得石子堆的个数减一, 那么平分成 i 堆需要的操作数为 n - i, 所以最终输出的答案为 n - i. 我们只需要枚举找到这个最大的 i 即可.

判断石子堆能否合并, 题目给出了一个良好的性质: 仅可以合并两个相邻的元素, 也就是说, 合并的部分是一段连续的区间, 我们就可以用一个变量 s 来累加石子堆, 从 a[0] 开始累加, 并判断如果 s == cnt, 那么重置 s = 0; 如果大于 0, 说明我们假设的 cnt 不成立. 如果能够遍历完 a, 则说明可以平分成 i 份.

本题一定有解, 因为 i = 1 一定成立.

奶牛大学

导航: USACO 2022 December Contest, Bronze Problem 1. Cow College

我们会首先会对输入进行排序, 使得 \(c_0 \leqslant c_1 \leqslant c_2 \cdots \leqslant c_n\), 方便我们进一步讨论.

首先可以证明, 选取的学费 \(x \in \{c_0, c_1, \cdots, c_n \}\). 可以反证. 假设 \(c_{i}<x<c_{i+1}\), 那么收取的总费用 \(y = x\cdot (n - i) < c_{i}\cdot(n - i)\), 需要比较的仅是 \(c_{i}\) 和 \(c_{i+1}\) 情况下的收取总费用. 对 \(c\) 从 0 到 n 枚举即可.

这题会卡int, 算收取总费用的时候要转换成long long.

选数异或

导航: 第十三届蓝桥杯省赛C++A/C/研究生组 Problem D

目标: 在数组 \(a\) 中找到满足 \(p_i\oplus q_i = x\) 的最小区间 \([p_i,q_i]\), 判断每次询问的 \([l,r]\) 是否使得 \([a_l\dots a_r]\) 包含任一 \([p_i,q_i]\).

性质 1 如果 p 符合条件, 那么 p ^ x 一定存在于数组.

证明 利用异或运算的性质

\[ p\oplus q = x \iff q = p \oplus x\]

而 q 在数组里, 那么 p ^ x 存在. 换过来说, 如果 q ^ x 存在, 则能判定 p 存在. 利用这一点, 枚举 i, 然后找到距离 \(q_i\) 最近的一个 \(p_i\) 的位置, 我们记函数 \(f(i)\), 它代表 \(a_i\) 左侧与 \(a_i\) 最近的一个配对数, 并约定, 如果左侧不存在配对, 那么 \(f(i) = 0\).

模拟样例:

模拟

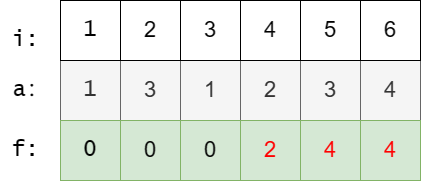
性质 2 原问题等价于: 判断 \(f(r) \geqslant l\).

证明 \(f(r)\) 表示 \(a_r\) 左侧最近的一个匹配数下标, 若存在, 那么一定存在 \(q \leqslant r\), 且 \(f(r)\) 大小为 \([1,r]\) 中最大的 \(p\) 下标. 记 \(i(x)\) 为元素 \(x\) 在数组中的下标位置. 即能找到一个 \(p\) 满足 \(i(p) \geqslant l\), 使得 \(l \leqslant i(p) < i(q) \leqslant r \iff \{p\dots q\}\subseteq a[l\dots r]\).

下一步就是求出 \(f(i)\) 的递推表达式. 如果在 \([1,r]\) 找到了新的匹配数 \(p'\), 那么就更新 \(f(i) = i(p')\), 否则 \(f(i) = f(i-1)\).

利用性质1, 可以利用一个哈希表. 如果哈希表内不存在 a[i] ^ x 的值, 那么会返回 0. 因为返回的是数值, 我们可以取 f(i - 1) 和 hash(a[i] ^ x) 的最大值作为 f(i).

下面的代码在处理输入时做了一些静态优化:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
const int M = 1 >> 20 + 5;
int n, m, x;
int a[M], dp[N];

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> m >> x;

    for (int i = 1; i <= n; i++)
    {
        int t;
        cin >> t;
        dp[i] = max(dp[i - 1], a[t ^ x]);
        a[t] = i;
    }

    while (m--)
    {
        int l, r;
        cin >> l >> r;
        cout << (dp[r] >= l ? "yes" : "no") << endl;
    }

    return 0;
}

数位排序

导航: 第十三届蓝桥杯省赛C++C组 数位排序

本题自定义实现一个比较函数, 然后STL sort即可.

但求数位和不能放在 cmp 里, 会TLE. 原因是sort的实现会进行 n 次 cmp 操作, 而 cmp 有 c = 10^1 级别的操作数, sort 时间复杂度为 O(n logn), 最大数据量 n = 10^6, 那么操作数约有 10 * 10 * 10^6 = 10^8, 就会卡时间.

在本地测试0.98s, 非常惊险, 但放oj平台TLE了.

所以我们需要预处理求 1~n 的数位和, 并保存到另一个数组里. 更优解是写一个结构体, 储存这个值和它的数位和, 然后对结构体数组排序.

使用排序预处理可以降低求解问题所需要的时间复杂度. 本质上这属于以空间换时间的一个平衡.

这样能少乘一个常数. 最大负载实际运行时间约为 0.23s.

重新排序

导航: 第十三届蓝桥杯省赛C++C组 H: 重新排序

本题类似于NOIP 2012 国王游戏 以及 P2123 皇后游戏. 题解可以参考: 浅谈邻项交换排序的应用以及需要注意的问题

贪心可以知道, 求和次数最多的位置, 重排后, 应当对应最大值. 这个可以通过邻项交换法证明.

一个想法是构造一个结构体, 包含值和这个位置被求和的次数, 然后对其排序.

但我们也可以构造两个数组, 对两个数组进行排序, 最后只用计算 a[i] * b[i] 的和就可以了, 甚至不用计算 [1,n] 上的前缀和, 因为如果一段区间如果没有被求和, b[i] = 0, 那么 sum += 0.

求 b[i], 利用每一组的 l, r 可以求得数组中各个元素被求和了多少次. 让 [l,r] 中的数据加上一个相同的数, 快速做法是差分.

技能升级

导航: 第十三届蓝桥杯省赛C++C组 倒数第二题

类似问题: 鱼塘钓鱼

钓鱼数量只和在某一鱼塘待的时间相关(因为不会折返). 我们要做的是以下几件事:

  • 枚举最远钓到哪个鱼塘(确定路上花费的时间)
  • 总钓鱼时间 n = T - 走的时间
  • 已知总钓鱼时间 n, 分配各个鱼塘, 求最大和, 即三个数组排序, 求前n元素的和. 用多路归并排序

这道题用的相同的思路: 求出堆前 m 个最大的元素的和s, 可以证明 s 就是最优解. 然而爆TLE, 原因是堆优化复杂度为O(m log n), 而 m 可以取到 2e9. 如果要解决本题, 那算法复杂度必须要 log m 或者和 m 无关.

换一种思路, 如果能找到归并后的数组中第 m 个数 x, 以及每个技能升级的次数t, 我们可以用 O(n) 的时间(多次利用等差数列的求和)计算前 m 项数的和:

1
res += sum(a[i], b[i], t);

数组按从大到小排序, 我们可以发现 \(\geqslant x\) 的数的个数 \(\geqslant m\), 也就表示 $x + 1 $ 的数 \(< m\) 个, 答案具有二段性, 于是我们可以用二分快速找出 x, 并且它的复杂度为 O(log n).

二分检查的性质可以用一种更快速的方法判断, 我们假设 t 为当前技能升级的次数, 那么

\[a_i - (t-1)b_i \geqslant x \iff t = \lfloor\dfrac{a_i-x}{b_i}\rfloor + 1\]

只用判断 \(\sum t \geqslant m\) 即可.

如此编码

导航: 27th CCF CSP认证 官网

考察对编码系统的理解, 我觉得还挺有意思的.

我们知道, 十进制数可以表示为

\[m = \sum^{n}_{i=1}10^{i-1}\cdot b_{i}\]

利用

\[ m \bmod{10^{j}} = \sum^{j}_{i=1}10^{i-1}\cdot b_{i} = m \bmod{10^{j - 1}} + 10^{j - 1} \cdot b^{j}\]

记 \(p_i = m \bmod{10^{i}}\), 那么

\[b_j = \frac{p_j - p_{j-1}}{10^{j-1}}\]

模拟样例: 假设 \(m = 177\), \(j = 2\), 那么 \(b_1 = \dfrac{7 - 0}{1} = 7\), \(b_{2} = \dfrac{77 - 7}{10} = 7\), \(b_3 = \dfrac{177 - 77}{100} = 1\).

这个算法的关键在于下面的数学表达式:

\[m \bmod c_{j}=\sum_{i=1}^{j} c_{i-1} \times b_{i}\]

读取各数位的算法可以写成:

1
2
3
4
for (int i = 1; i <= n; i++) {
    p[i] = m % c[i];    // c[i] = 10^i
    b[i] = (p[i] - p[i - 1]) / c[i - 1];
}

相比于原本求数位的方法要麻烦许多. 但这个算法的好处在于对一个变化的 c, 只要存在 c 和 i 的一个映射关系, 就一定能求出 b[i].

按照本题的意思, 可以先计算 a[i] 的前缀乘积 c[i], 然后利用上面的公式即可. 实际操作可以做一些静态处理, 例如 p[i] 在计算前缀乘积时就可以预处理了.

这种做法并不关注本题 c[i] 为 a[i] 的累乘这一性质. 另外一个常用的公式:

\[m=c_{i}\left\lfloor\frac{m}{c_{i}}\right\rfloor+m \bmod c_{i}\]

如果你能发现

\[m = \sum_{i=1}^{n}\left(b_{i} \times \prod_{j=1}^{i-1} a_{j}\right) = a_{1}\left[a_{2}\left(a_{3} \times \cdots+b_{3}\right)+b_{2}\right]+b_{1}\]

再利用 \(m=a_{i}\left\lfloor\frac{m}{a_{i}}\right\rfloor+m \bmod a_{i}\) 的性质, 发现 \(b_i = m \bmod a_i\). 之后只需要更新一下 \(m' = \dfrac{m - b_i}{a_i}\) 就可以计算 \(b_{i+1}\) 的值了.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <bits/stdc++.h>
using namespace std;
int n, m, x, i;
int main()
{
    cin >> n >> m;
    for (i = 1; i <= n; i++)
    {
        cin >> x;
        cout << m % x << ' ';
        m /= x;
    }
    return 0;
}

出行计划

原题出处: 25th CCF CSP 认证

朴素解法: 判断 \(t_i - (q+k) \leqslant c_i - 1\), 同时要保证 \(t_i \geqslant q + k\).

这样做的复杂度为 O(mn), 数量级为 10^10, 明显TLE. 尝试空间换时间:

假设 \(p_i\) 表示第 \(i\) 时刻出行, 且此时刻核酸结果对 \(c_i\) 有效, 可行的方案个数.

这样做的好处是面对多例查询, 可以用 a[q + k] 快速得出结果. 这样算法复杂度就降低成 O(n + m), 变为可计算的问题了. 下面的问题在于怎么用 O(n) 的复杂度求出这个 a 数组.

在我们的假设中, i 时刻核酸结果对 c[i] 有效, 首先可以知道 t[i] 时刻的可行的方案数需要加一, 考虑 t[i] 恰好是核酸有效的最后一个时刻. 往前倒推 c[i] 个时刻, 从 t[i] - c[i] + 1 开始, 这一段区间上的方案数也需要加一, 考虑 t[i] - c[i] + 1 恰好是核酸结果刚出的时刻.

一个问题是如果 t[i] < c[i], 此时下标会得到一个负数. 我们只需要默认最远回退到下标 1 即可.

一组 t, c 得到一段区间 [l, r], 让 a[l...r] 的元素自增1, 这个操作可以通过差分实现.

左孩子右兄弟

导航: 第十二届蓝桥杯省赛第一场 C++ A/C 组, 第十二届蓝桥杯省赛第一场 JAVA A/C 组

这道题难点在于看懂题意. 对于一个根节点 u, 它的子节点必然大于父节点 u, 子树处于左侧, 子树的第一个节点即为第一个儿子, 儿子的右兄弟则为 u 的第二个儿子, 以此类推, 直到 p[i] <= u.

模拟样例

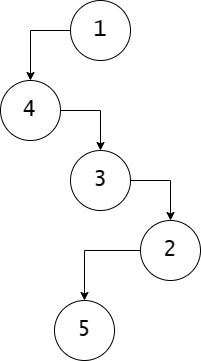
例如, 在上面的例子中, 4, 3, 2 都大于 1, 因此它们都是 1 的儿子; 3, 2 小于 4, 作为 4 的右兄弟; 而 5 因为大于 2, 因此是 2 的儿子.

关注一个性质: 4, 3, 2 之间的顺序是可以互换的. 我们并不强求右兄弟的值小于当前节点, 因为仍然满足都小于 1 的条件(即便切换顺序以后, 可以多出新的分支)

我们考虑 h 为当前节点子树的高度, 假设 u 的儿子为 a, b, 那么 h(a) 表示 a 节点子树的高度. 例如在上面的例子中, 考虑 a = 2, h(a) = 1. 我们计算的答案为 h(2) + 3 = 4.

我们要求的是 \(f(u) = \max \{ h(s_i) + c_i \}\), 其中 \(c_i\) 是当前节点的高度. 那么就可以按照树形dp的方法处理: DFS u 的所有子节点, 求出 f(u), 答案即为 f(1)(根节点).

如果你乐意, 可以证明 \(h(s_i) + c_i\) 的最大值可以在 \(c_i\) 为最大值时取到, 考虑反证法. 并且由于右兄弟之间可以互换的性质, \(c_i\) 取最大值, 即 u 子节点的数量 cnt(即上例中节点 2 位于子树的最高处).

我们只需要求出子节点中的 \(h_{max} + cnt\) 即可.

后记

这次的寒假每日一题, 总的来说, 还是收获不小的.

以做代练确实是很好的一种做法, 因为当我们上手一道题感到一筹莫展的时候, 你会自主地去挖掘这道题目的背景, 以及需要掌握的预备知识. 对于算法新人来说, 这么做比一味地刷视频打卡, 学习效率要高很多, 最主要是涉及的知识更广: 这里有数论, 有dp, 有贪心, 有数据结构, 也有基础——提前预习, 或者复习某些已经刷过的知识点, 真的获益不少.