前缀函数和KMP算法

发表于 2022-12-21 更新于 2023-03-11 分类于数据结构本文字数： 3.3k 阅读时长 ≈ 12 分钟

做期末大作业里面有个字符串匹配的问题, 用暴力算法做完觉得不够爽, 于是自找的麻烦.

想用最简明的方式去解释这个较为抽象的算法! 事实上明白了一个道理: 缺乏数学的算法都是玄学, 只有数学证明了才能让人心服口服......

就好像物理规律, 如果数学上证明了成立, 你会感到无比安心. 模拟样例终归比不了证明有说服力.

问题: 在一个文本串(s, 也称主串)中找到一个匹配串(p), 返回它在文本串中的下标. 如果无法匹配返回-1.

前言: 暴力解决问题

思路很明了: 用指针i遍历s, j遍历p. 具体的遍历过程

指针移动 s[i]是否匹配p[j]
1. 如果匹配, 则后移j指针, 比较p后继字符是否和s中的一致.
2. 如果不匹配, 那么后移i指针, 并将j指针重新设置为0.
终止条件 当j指针指向p最后一个字符, 说明匹配完成. 这时候就可以输出i - j的值, 作为匹配串在文本串中的索引.

int bf(char *s, char *p)
{
    int i = 0, j = 0;
    while (s[i] != '\0')
    {
        if (s[i] == p[j])
            i++, j++;
        else {
            i -= j; i++; j = 0;
        }
        if (p[j] == '\0')
            return i - j;
    }
    return -1;
}

时间复杂度分析: 考虑最坏情况, $O(|P| (|S|+|P|-1)) = O(|P||S|) $, 也就是 $O(nm)$.

预备知识

字符串基础

子串: 串中任意个连续的字符组成的子序列.

字符串前缀: 一个字符串的全部头部组合, 但不包括自身.

严格来说, KMP讨论的是字符串的真前缀.

例子: abcab 的前缀(集合)为 {a, ab, abc, abca}

同样的有字符串后缀, 按上面的例子, 后缀(集合)就应该为 {b, ab, cab, bcab}.

前缀函数

给定长度n的字符串s, 其前缀函数定义为长度为n的数组$\pi$, 其中$\pi[i]$是子串s[0...i]最长的相等前缀和后缀长度. 具体来说:

$\pi[0]$ = 0. 因为此时无前缀及后缀.(对于部分实现可能会规定其为-1)
如果子串有一对相同的前后缀, 那么 $\pi[i]$ 就等于这个前缀(或后缀)的长度. 如果存在多对, 那么就是它们中的最大值.

例如, 对于abcab, pi[0] = 0, pi[1] = 0, pi[2] = 0, pi[3] = 1, pi[4] = 2. 那么它的前缀函数就为 {0, 0, 0, 1, 2}.

优雅求得一个字符串的前缀函数是件并不容易的事情. 我们会在下面接着讨论.

KMP 算法就是状态机

所谓算法, 就是把暴力穷举优化成聪明的枚举. 这句话对KMP算法同样适用: 利用匹配失败后的信息, 减少模式串和文本串的匹配次数.

在暴力算法中, 每当s[i] != p[j], j 被重新设置为0, 而i回溯到匹配前的位置, 同时只自增1. 我们的目的是: 减少算法复杂度O(nm)中的n, 也即减少不必要的匹配次数, 换句话说, 要么动态增加i的步长; 要么不回溯i, 让i一直自增下去.

为了实现这一点, 我们需要利用一切匹配失败前获取的信息. 而在匹配失败之前, 有字符是匹配的: 文本串的一部分等于模式串的一段前缀.

如果我们能跳过不可能成功匹配的字段, 就可以有效减少匹配的次数.

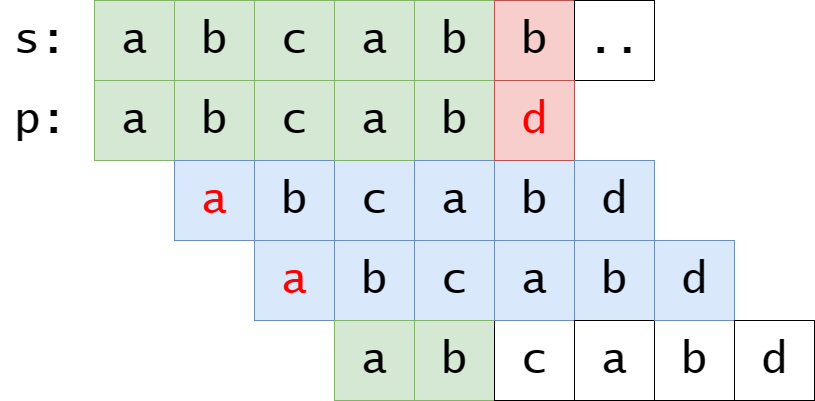
如图所示, 如果能够跳过中间标蓝的不必要的匹配(第一个字符都失败了, 明显不可能匹配成功), 就可以大幅减少我们的匹配次数.

我们要做的实际上就一件事: 让文本串的一段对上匹配串的一段前缀, 而且跳过越多不必要的匹配越好. 跳过的这个长度在我们匹配失败前就应确定, 根据已有的信息, 这个最优长度是 s子串的后缀和p子串的前缀交集中最长元素的长度. 在上例中, 就是 $\text{\{a,ab,abc,abca\}}\cap \text{\{b, ab, cab, bcab\}} = \text{\{ab\}}$ 的长度, 也就是2, 表示的含义也即: 让p的ab对上s的ab.

而且, 由于在匹配失败之前, 匹配都是成功的, 我们可以得到另外一个信息是 s串的部分子串等同于p串的部分子串, 那么, 此时s子串的后缀和p子串的前缀交集中最长元素的长度, 就等同于 p子串的最大前后缀长度, 也就是p串的前缀函数.

这是巨大的一步! 因为我们可以在s和p进行匹配之前就计算出p每一次向右移动的长度.

在KMP算法中, 我们记这个数组为next数组.

在下面的算法中, 我们依然用i表示指向s的字符下标, j表示指向p的字符下标.

相较于暴力算法, 我们优化的点主要在于j != 0的情况: 让i不回溯, 只让j回溯. i不动, 让p[next[j - 1]]和s中方才匹配失败的字符s[i]进行比较. 假使这一步又失败了, 我们还是回溯j, 找s[i] == p[j], 直到j为0, 也就意味着s和p没有交集了. 这时, 移动i, 进行新一轮的匹配. 注意, 这是KMP最差的情况: i++, j=0, 这和暴力算法实际上没有多少区别. 但通过j = next[j - 1]的状态转移, 我们减少了大量的匹配次数!

一切操作, 只是简单地改变i和j状态——KMP算法本质上就是一个优化了的状态机!

int next[N];
int kmp(char *s, char *p) {
    int i = 0, j = 0;
    while(s[i] != '\0')
    {
        if(s[i] == p[j])
            i++, j++;
        else if (j)
            j = next[j - 1];
        else
            i++;
        if(p[j] == '\0')
            return i - j;
    } 
}

多例查询你可以这么写:

if(p[j] == '\0') {
    cout << i - j << ' ';
    j = next[j];
}

如果你是用 C++ 写的代码, 建议将 next 数组命名为 ne, 否则容易和 STL 库的命名冲突.

至于next数组, 我们其实也可以暴力解决:

void getNext(char *p) {
    int n = strlen(p);
    for (int i = 1; i < n; i++) {
        for (int j = i; j >= 0; j--) {
            int match = 1;
            for (int k = 0; k < j; k++) {
                if (p[k] != p[i - j + 1 + k]) {
                    match = 0;
                    break;
                }
            }
            if (match) {
                next[i] = j;
                break;
            }
        }
    }
}

暴力算法的时间复杂度是O(n^3), 数据量大必爆, 而且非常丑陋, 这对KMP这样优雅的算法简直就是致命的. 下面, 我们就来看看怎么才能优雅地计算next数组.

优雅计算前缀函数

就像动态规划dp找到状态转移方程, 找到前缀函数的递推公式将是我们解题的关键.

仔细观察前缀函数, 第一个重要性质就是: 相邻的前缀函数值最大增加 1.

不要忘记我们对前缀函数的定义是: 最长的相等前缀和后缀长度.

那么, 这个性质可以这么思考: 要取一个尽可能大的$\pi[i]$, 必然要求新增的 s[i] 能和对应的字符匹配, 也即 $s[i] = s[\pi[i-1]]$, 此时 $\pi[i] = \pi[i-1] + 1$. 例如: 上图中, i = 5的位置(c), 比较的是 i = pi[4] = 2 的位置(c), 即相等前缀的下一字符, 因为相等, 所以pi[5] = pi[4] + 1; i = 11(c) 比较的是 i = pi[10] = 5(c), 相等所以加一.

下一步是考虑 $s[i] \neq s[\pi[i-1]]$ 的情况. 如图所示, 我们期望, 当s[i]失配时, 对于子串s[0...i-1], 依然能找到仅次于 $\pi[i-1]$ 的第二长度 j, 使得在位置 i-1 的前缀性质依然保持, 也即 s[0...j-1] = s[i-j...i-1].

数学看上去有些抽象, 举个例子: 如图, i = 11 时失配了, 对于子串 abcabdabcab, 依然能找到比 $\pi[10] = 5$ 小的第二长度 j (在这里是 2), 使得 i = 10 的前缀性质依然保持, 这里找到的公共前后缀为ab.

如果我们找到了这样的j, 那么就只需要比较s[i]和s[j].

如果它们相等, 就有 $\pi[i] = j + 1$. 在上面的例子中, 因为 s[11] = s[2], 因此 $\pi[11] = 3$. 此时最大前后缀为abc.
如果它们不相等, 假设本例中的 s[11] = 'a', 根据上面的讨论, 我们需要再找到一个仅次于 $j$ 的 $j^{(2)}$, 使得前缀性质得以保持. 此时 $j^{(2)}$ 只能为0了, 因为s[i] = s[0], 所以pi[11] = 1.

以此类推, 按照数学归纳, 直到 $j^{(n)} = 0$ 时我们结束寻找第二长度, 并且我们可以知道, 如果 $s[i]\neq s[0]$, 那么 $\pi[i] = 0$, 正如本例中的i = 5(d不匹配任何一个字符).

前缀函数另一个重要的性质, 也就是j实际上等价于子串$s[0...\pi[i - 1] - 1]$的前缀函数值, 也即

\[j = \pi[\pi[i - 1] - 1] \]

上例中, 也即i = 5处pi的值, 也就是我们已经求得的 2! 同理, $j^{(2)} = \pi[j-1]$, 那么归纳可得 $j^{(n)} = \pi[j^{(n-1)}-1]$.

于是我们就有了最终的代码:

int next[N] = {0};
void getNext(char *p) {
    int i = 1, j = 0;
    while (p[i] != '\0') {
        if(p[i] == p[j]) {
            next[i] = next[i - 1] + 1;
            i++, j++;
        }
        else if(j)
            j = next[j - 1];
        else {
            next[i] = 0;
            i++;
        }
    }
}

调整下代码, 写成双指针的形式, 就可以得到更符合算法竞赛的算法啦! (见下)

各位可以揣读一下这段代码的精妙, 甚至框架和KMP搜索惊人的一致! (都是改变状态实现)

例题

AcWing 141. 周期 next 数组的另一种解释.

首先要理解什么是字符串的周期. 给出一个样例: aa, 由 2 个 a 的循环节构成, 它的周期为 1. aab 就不存在这样的循环节, 也即不存在周期. aabaab 由 2 个 aab 的循环节构成, 它的周期为 3.

严格些的定义: 对字符串 $s$ 和 $0 < p \leqslant |s|$, 若 $s[i] = s[i+p]$ 对所有 $i\in[0,|s|-p-1]$ 成立, 那么 $p$ 是 $s$ 的周期.

我们再给出另一个概念的定义: 对字符串 $s$ 和 $0 < r \leqslant |s|$, 若 $s$ 和 $r$ 的前缀和长度为 $r$ 的后缀相等, 就称 $s$ 长度为 $r$ 的前缀是 $s$ 串的border.

推论: $s$ 有长度为 $r$ 的border可以推出 $|s| - r$ 为 $s$ 的周期.

例如 bbabbab 满足一个 Border $r=4$ "bbab" 且 $p=3$, 满足 $r+p=|S|=7$.

推论告诉我们求一个字符串的周期就等同于求Border.

按照前缀函数的定义, 即可得到 $s$ 所有的border长度, 即 $\pi[n-1],\pi[\pi[n-1]-1],\dots$, 且 $\pi[n-1]$ 是非平凡的最大Border. 于是我们可以在 $O(n)$ 的时间内计算出所有 $s$ 的周期, 且知 $n - \pi[n-1]$ 是 $s$ 的最小正周期.

#include <bits/stdc++.h>
using namespace std;

const int N = 1e6 + 5;
int n, m;
char s[N];
int ne[N];

signed main()
{
    while (scanf("%d", &n) == 1 && n != 0)
    {
        scanf("%s", s);

        for (int i = 1; i <= n; i++)
        {
            int j = ne[i - 1];
            while (j > 0 && s[i] != s[j])
            {
                j = ne[j - 1];
            }
            if (s[i] == s[j])
                j++;
            ne[i] = j;
        }
        printf("Test case #%d\n", ++m);
        for (int i = 2; i <= n; i++)
        {
            int T = i - ne[i - 1];
            int k = i / T;
            if (i % T == 0 && k > 1)
                printf("%d %d\n", i, k);
        }
        printf("\n");
    }

    return 0;
}

其它应用: 统计每个前缀的出现次数, 一个字符串中本质不同子串的数目, 字符串压缩, 根据前缀函数构建一个自动机

模板

正文部分给出的是C语言实现版本. 下面给出主流算法竞赛中使用的C++实现方式.

来源: OI-wiki 前缀函数和KMP算法

vector<int> prefix_function(string s)
{
    int n = (int)s.length();
    vector<int> pi(n);
    for (int i = 1; i < n; i++)
    {
        int j = pi[i - 1];
        // 不匹配且 j 不为 0
        while (j > 0 && s[i] != s[j])
            j = pi[j - 1];  // 满足前缀性质的第二长度
        // 匹配
        if (s[i] == s[j])
            j++;
        pi[i] = j;
    }
    return pi;
}

来源: AcWing 831.KMP字符串

#include <bits/stdc++.h>
const int N = 1e6 + 5;
using namespace std;

char p[N], s[N];
int ne[N];
int n, m;

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n >> p >> m >> s;
    ne[0] = -1;

    for (int i = 1, j = -1; i < n; i++)
    {
        while (j != -1 && p[i] != p[j + 1])
            j = ne[j];
        if (p[i] == p[j + 1])
            j++;
        ne[i] = j;
    }

    for (int i = 0, j = -1; i < m; ++i)
    {
        while (j != -1 && s[i] != p[j + 1])
        {
            j = ne[j];
        }
        if (s[i] == p[j + 1])
        {
            j ++;
        }
        if (j == n - 1)
        {
            cout << i - j << ' ';
            j = ne[j];
        }
    }
    return 0;
}

参考

[1]. OI-wiki 前缀函数和KMP算法

[2]. 邓俊辉. 数据结构(C++语言版). 北京: 清华大学出版社, 2013.09第三版. ISBN: 7-302-33064-6. P331. KMP算法

[3]. 木子喵neko. 【喵的算法课】KMP算法【7期】

[4]. calabash_boy (注: NJU final爷). 牛客竞赛字符串专题班Trie（字典树多模式匹配）. 2022年1月15日.